Welcome to the resource topic for 2022/887
Title:
Round-Optimal Black-Box Protocol Compilers
Authors: Yuval Ishai, Dakshita Khurana, Amit Sahai, and Akshayaram Srinivasan
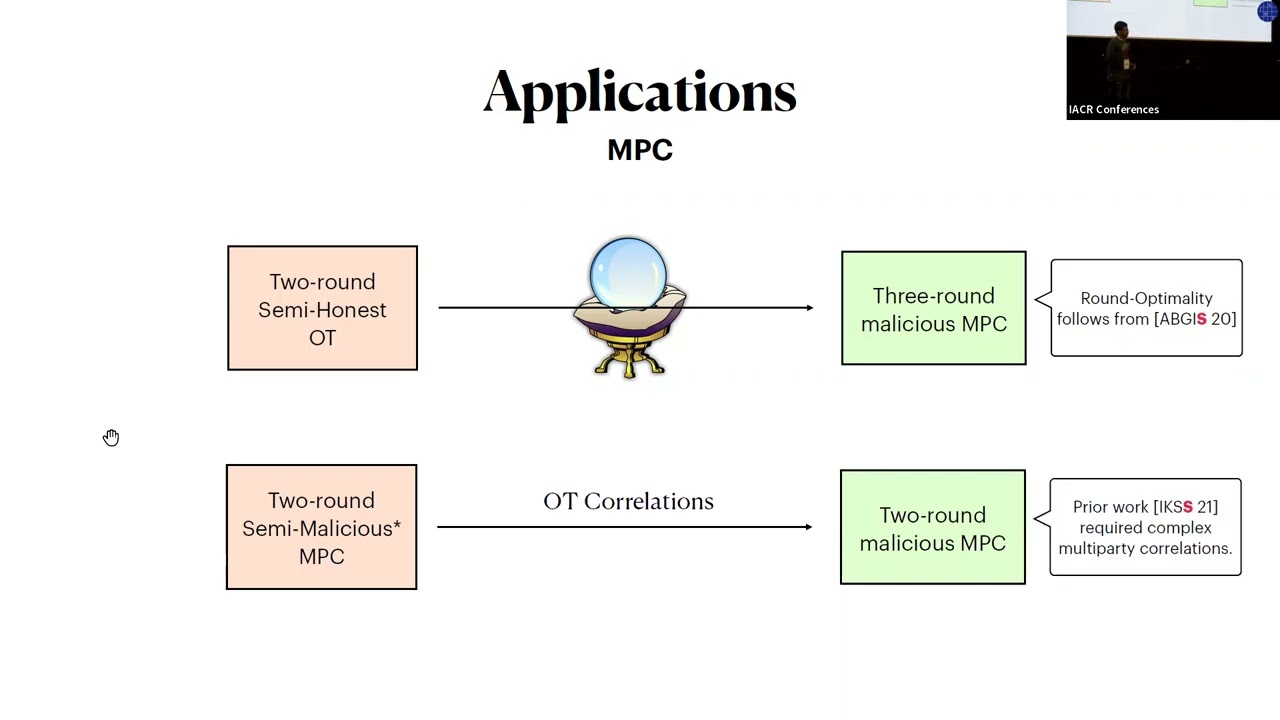
Abstract:We give black-box, round-optimal protocol compilers from semi-honest security to malicious security in the Random Oracle Model (ROM) and in the 1-out-of-2 oblivious transfer (OT) correlations model. We use our compilers to obtain the following black-box constructions of general-purpose protocols for secure computation tolerating static, malicious corruptions of all-but-one participants: \begin{itemize} \item A two-round, two-party protocol in the random oracle model, making black-box use of a two-round semi-honest secure protocol. Prior to our work, such a result was not known even for special functionalities such as OT. As an application, we get efficient constructions of two-round malicious OT/OLE in the random oracle model based on a black-box use of two-round semi-honest OT/OLE. \item A three-round multiparty protocol in the random oracle model, making a black-box use of two-round semi-honest OT. This protocol matches a known round complexity lower bound due to Applebaum et al. (ITCS 2020) and is based on a minimal cryptographic primitive. \item A two-round multiparty protocol in the OT correlations model, making a black-box use of a semi-malicious protocol. This improves over a similar protocol of the authors (Crypto 2021) by eliminating an adaptive security requirement and replacing nonstandard multiparty OT correlations by standard ones. As an application, we get 2-round protocols for arithmetic branching programs that make a black-box use of the underlying field. \end{itemize} As a contribution of independent interest, we provide a new variant of the IPS compiler (Ishai, Prabhakaran and Sahai, Crypto 2008) in the two-round setting, where we relax requirements on the IPS inner protocol'' by strengthening the outer protocol’'.
ePrint: https://eprint.iacr.org/2022/887
Talk: https://www.youtube.com/watch?v=HKfAMYaqItM
Slides: https://iacr.org/submit/files/slides/2022/eurocrypt/eurocrypt2022/271/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .