Welcome to the resource topic for 2022/818
Title:
Provably Secure Reflection Ciphers
Authors: Tim Beyne and Yu Long Chen
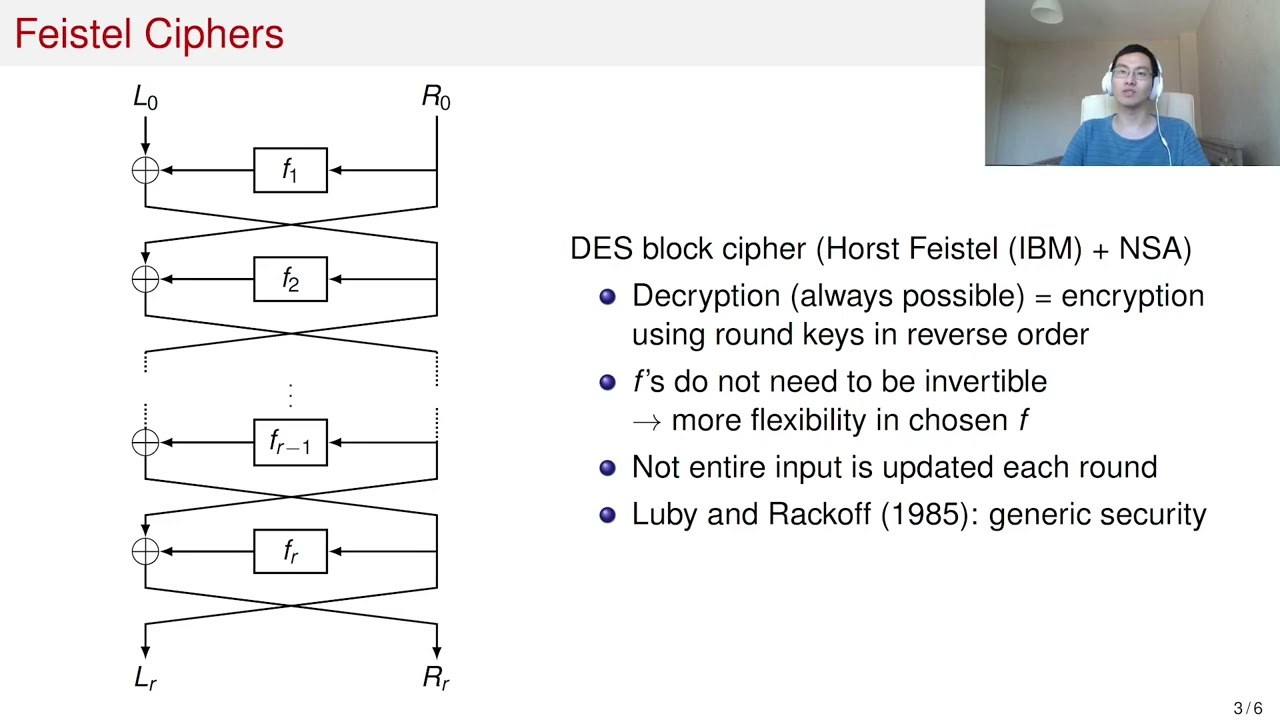
Abstract:This paper provides the first analysis of reflection ciphers such as PRINCE from a provable security viewpoint. As a first contribution, we initiate the study of key-alternating reflection ciphers in the ideal permutation model. Specifically, we prove the security of the two-round case and give matching attacks. The resulting security bound takes form (O(qp^2/2^{2n}+q^2/2^n)), where (q) is the number of construction evaluations and (p) is the number of direct adversarial queries to the underlying permutation. Since the two-round construction already achieves an interesting security lower bound, this result can also be of interest for the construction of reflection ciphers based on a single public permutation. Our second contribution is a generic key-length extension method for reflection ciphers. It provides an attractive alternative to the FX construction, which is used by PRINCE and other concrete key-alternating reflection ciphers. We show that our construction leads to better security with minimal changes to existing designs. The security proof is in the ideal cipher model and relies on a reduction to the two-round Even-Mansour cipher with a single round key. In order to obtain the desired result, we sharpen the bad-transcript analysis and consequently improve the best-known bounds for the single-key Even-Mansour cipher with two rounds. This improvement is enabled by a new sum-capture theorem that is of independent interest.
ePrint: https://eprint.iacr.org/2022/818
Talk: https://www.youtube.com/watch?v=oaN923Ato_0
Slides: https://iacr.org/submit/files/slides/2022/crypto/crypto2022/258/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .