[Resource Topic] 2022/1013: Dynamic Local Searchable Symmetric Encryption

Resource Cryptographic protocols
#1

Welcome to the resource topic for 2022/1013

Title:
Dynamic Local Searchable Symmetric Encryption

Authors: Brice Minaud, Michael Reichle

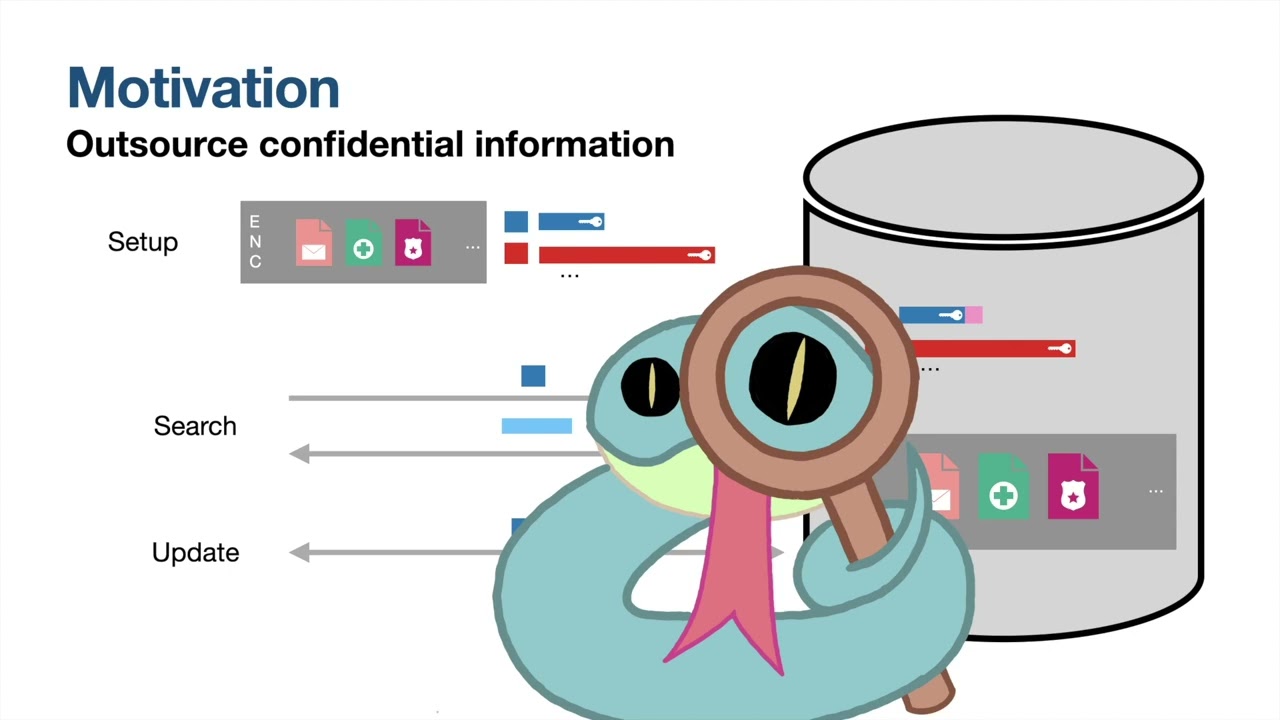
Abstract:

In this article, we tackle for the first time the problem of dynamic memory-efficient Searchable Symmetric Encryption (SSE). In the term “memory-efficient” SSE, we encompass both the goals of local SSE, and page-efficient SSE. The centerpiece of our approach is a new connection between those two goals. We introduce a map, called the Generic Local Transform, which takes as input a page-efficient SSE scheme with certain special features, and outputs an SSE scheme with strong locality properties. We obtain several results.

  1. First, we build a dynamic SSE scheme with storage efficiency O(1) and page efficiency only \tilde{O}(\log \log (N/p)), where p is the page size, called LayeredSSE. The main technique behind LayeredSSE is a new weighted extension of the two-choice allocation process, of independent interest.

  2. Second, we introduce the Generic Local Transform, and combine it with LayeredSSE to build a dynamic SSE scheme with storage efficiency O(1), locality O(1), and read efficiency \tilde{O}(\log\log N), under the condition that the longest list is of size O(N^{1-1/\log \log \lambda}). This matches, in every respect, the purely static construction of Asharov et al. from STOC 2016: dynamism comes at no extra cost.

  3. Finally, by applying the Generic Local Transform to a variant of the Tethys scheme by Bossuat et al. from Crypto 2021, we build an unconditional static SSE with storage efficiency O(1), locality O(1), and read efficiency O(\log^\varepsilon N), for an arbitrarily small constant \varepsilon > 0.
    To our knowledge, this is the construction that comes closest to the lower bound presented by Cash and Tessaro at Eurocrypt 2014.

ePrint: https://eprint.iacr.org/2022/1013

Talk: https://www.youtube.com/watch?v=RY5T2_00_cQ

Slides: https://iacr.org/submit/files/slides/2022/crypto/crypto2022/451/slides.pdf

See all topics related to this paper.

Feel free to post resources that are related to this paper below.

Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.

For more information, see the rules for Resource Topics .