Welcome to the resource topic for 2022/1011
Title:
Structure-Aware Private Set Intersection, With Applications to Fuzzy Matching
Authors: Gayathri Garimella, Mike Rosulek, Jaspal Singh
Abstract:In two-party private set intersection (PSI), Alice holds a set X, Bob holds a set Y, and they learn (only) the contents of X \cap Y.
We introduce structure-aware PSI protocols, which take advantage of situations where Alice’s set X is publicly known to have a certain structure.
The goal of structure-aware PSI is to have communication that scales with the description size of Alice’s set, rather its cardinality.
We introduce a new generic paradigm for structure-aware PSI based on function secret-sharing (FSS).
In short, if there exists compact FSS for a class of structured sets, then there exists a semi-honest PSI protocol that supports this class of input sets, with communication cost proportional only to the FSS share size.
Several prior protocols for efficient (plain) PSI can be viewed as special cases of our new paradigm, with an implicit FSS for unstructured sets.
Our PSI protocol can be instantiated from a significantly weaker flavor of FSS, which has not been previously studied.
We develop several improved FSS techniques that take advantage of these relaxed requirements, and which are in some cases exponentially better than existing FSS.
Finally, we explore in depth a natural application of structure-aware PSI.
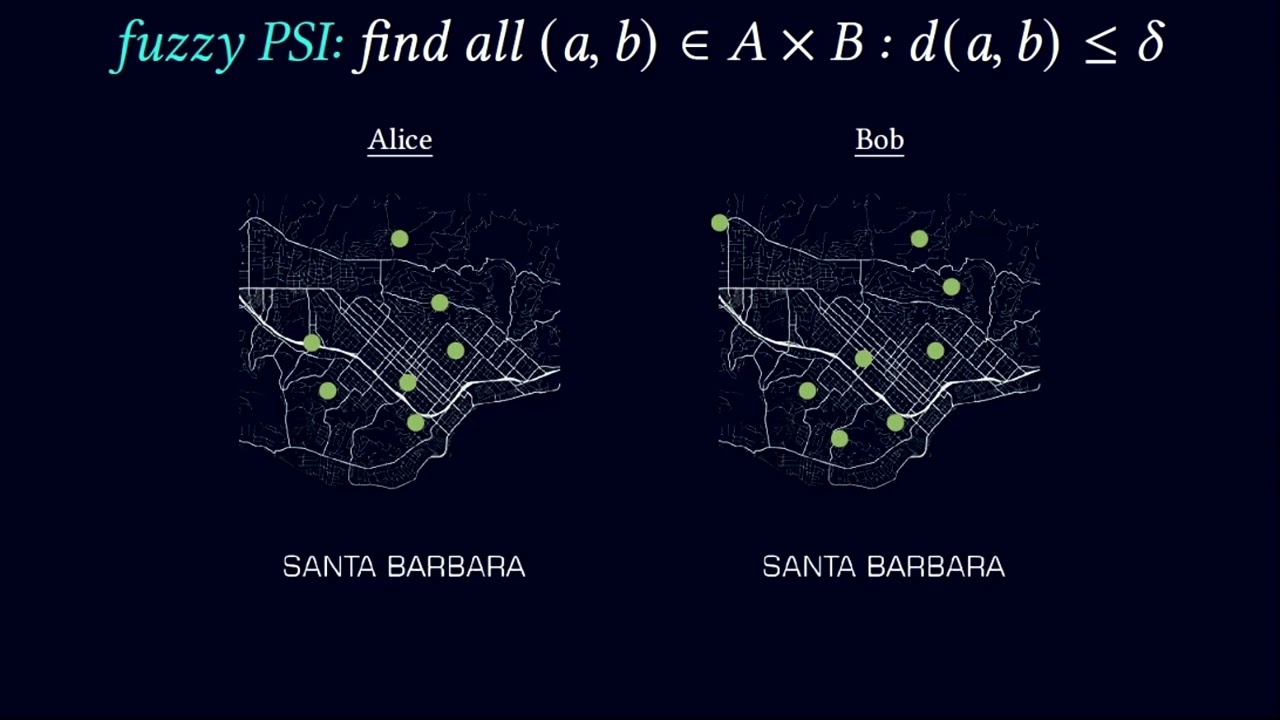
If Alice's set $X$ is the union of many radius-$\delta$ balls in some metric space, then an intersection between $X$ and $Y$ corresponds to fuzzy PSI, in which the parties learn which of their points are within distance $\delta$.
In structure-aware PSI, the communication cost scales with the number of balls in Alice's set, rather than their total volume.
Our techniques lead to efficient fuzzy PSI for $\ell_\infty$ and $\ell_1$ metrics (and approximations of $\ell_2$ metric) in high dimensions.
We implemented this fuzzy PSI protocol for 2-dimensional $\ell_\infty$ metrics.
For reasonable input sizes, our protocol requires 45--60% less time and 85% less communication than competing approaches that simply reduce the problem to plain PSI.
ePrint: https://eprint.iacr.org/2022/1011
Talk: https://www.youtube.com/watch?v=MWWbqtH1pOM
Slides: https://iacr.org/submit/files/slides/2022/crypto/crypto2022/6/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .