Welcome to the resource topic for 2022/1009
Title:
Time-Space Tradeoffs for Sponge Hashing: Attacks and Limitations for Short Collisions
Authors: Cody Freitag, Ashrujit Ghoshal, Ilan Komargodski
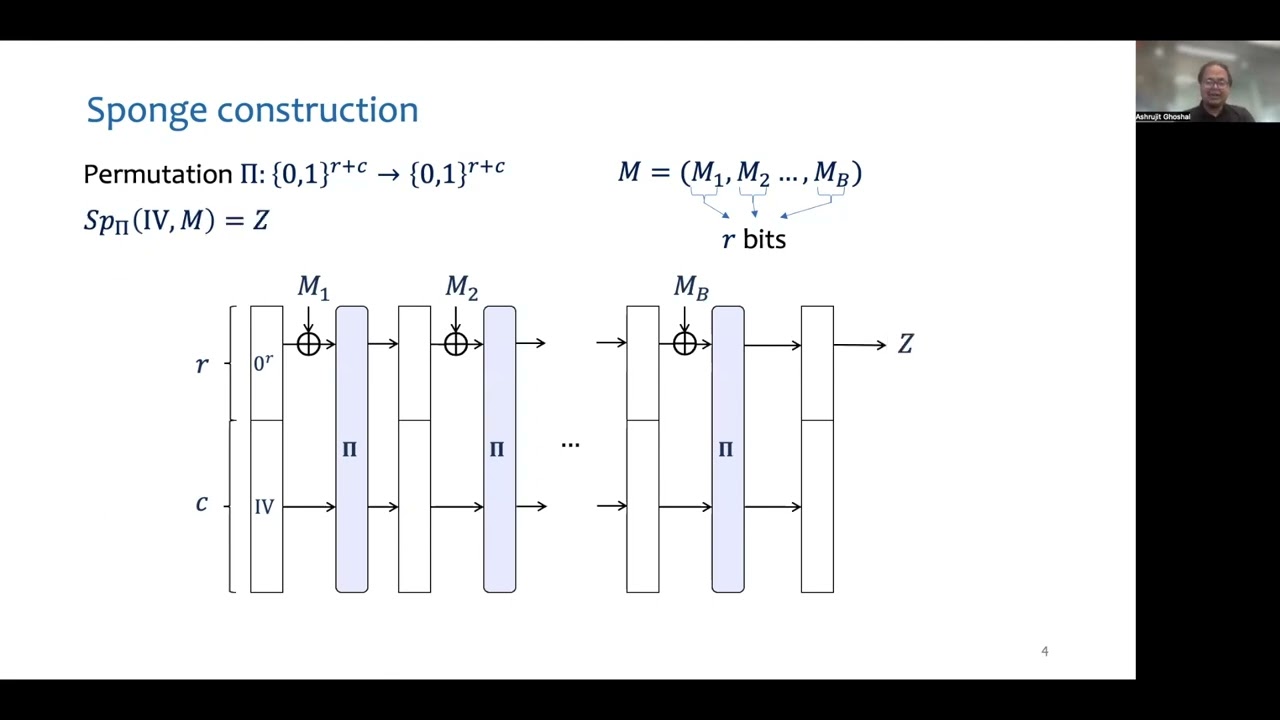
Abstract:Sponge hashing is a novel alternative to the popular Merkle-Damgård hashing design. The sponge construction has become increasingly popular in various applications, perhaps most notably, it underlies the SHA-3 hashing standard. Sponge hashing is parametrized by two numbers, r and c (bitrate and capacity, respectively), and by a fixed-size permutation on r+c bits. In this work, we study the collision resistance of sponge hashing instantiated with a random permutation by adversaries with arbitrary S-bit auxiliary advice input about the random permutation that make T online queries. Recent work by Coretti et al. (CRYPTO '18) showed that such adversaries can find collisions (with respect to a random c-bit initialization vector) with advantage \Theta(ST^2/2^c + T^2/ 2^{r}).
Although the above attack formally breaks collision resistance in some range of parameters, its practical relevance is limited since the resulting collision is very long (on the order of T blocks). Focusing on the task of finding short collisions, we study the complexity of finding a B-block collision for a given parameter B\ge 1. We give several new attacks and limitations. Most notably, we give a new attack that results in a single-block collision and has advantage
In certain range of parameters (e.g., ST^2>2^c), our attack outperforms the previously-known best attack. To the best of our knowledge, this is the first natural application for which sponge hashing is provably less secure than the corresponding instance of Merkle-Damgård hashing. Our attack relies on a novel connection between single-block collision finding in sponge hashing and the well-studied function inversion problem. We also give a general attack that works for any B\ge 2 and has advantage \Omega({STB}/{2^{c}} + {T^2}/{2^{\min\{r,c\}}}), adapting an idea of Akshima et al. (CRYPTO '20).
We complement the above attacks with bounds on the best possible attacks. Specifically, we prove that there is a qualitative jump in the advantage of best possible attacks for finding unbounded-length collisions and those for finding very short collisions. Most notably, we prove (via a highly non-trivial compression argument) that the above attack is optimal for B=2 in some range of parameters.
ePrint: https://eprint.iacr.org/2022/1009
Talk: https://www.youtube.com/watch?v=M4fIui6_X50
Slides: https://iacr.org/submit/files/slides/2022/crypto/crypto2022/294/slides.pptx
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .