Welcome to the resource topic for 2021/926
Title:
On Treewidth, Separators and Yao’s Garbling
Authors: Chethan Kamath, Karen Klein, Krzysztof Pietrzak
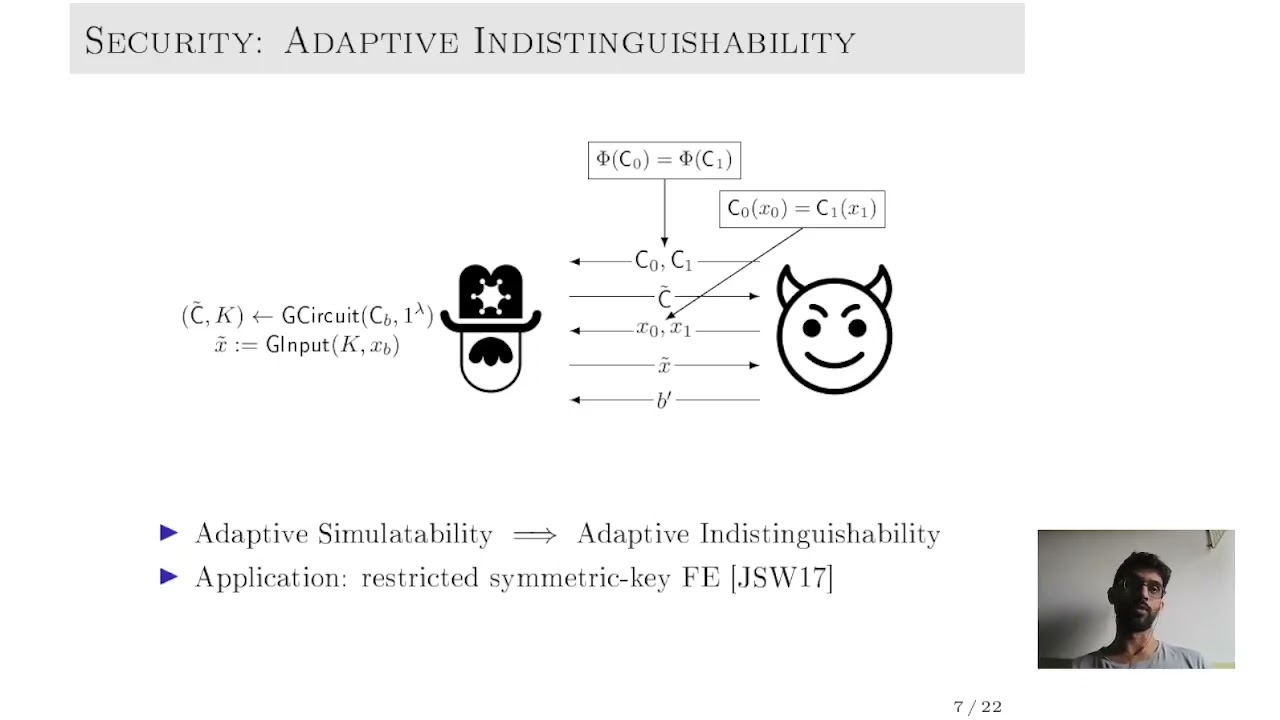
Abstract:We show that Yao’s garbling scheme is adaptively indistinguishable for the class of Boolean circuits of size S and treewidth w with only a S^O(w) loss in security. For instance, circuits with constant treewidth are as a result adaptively indistinguishable with only a polynomial loss. This (partially) complements a negative result of Applebaum et al. (Crypto 2013), which showed (assuming one-way functions) that Yao’s garbling scheme cannot be adaptively simulatable. As main technical contributions, we introduce a new pebble game that abstracts out our security reduction and then present a pebbling strategy for this game where the number of pebbles used is roughly O(d w log(S)), d being the fan-out of the circuit. The design of the strategy relies on separators, a graph-theoretic notion with connections to circuit complexity.
ePrint: https://eprint.iacr.org/2021/926
Talk: https://www.youtube.com/watch?v=GWbYGkGTVyY
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .