Welcome to the resource topic for 2021/572
Title:
Sine Series Approximation of the Mod Function for Bootstrapping of Approximate HE
Authors: Charanjit Singh Jutla, Nathan Manohar
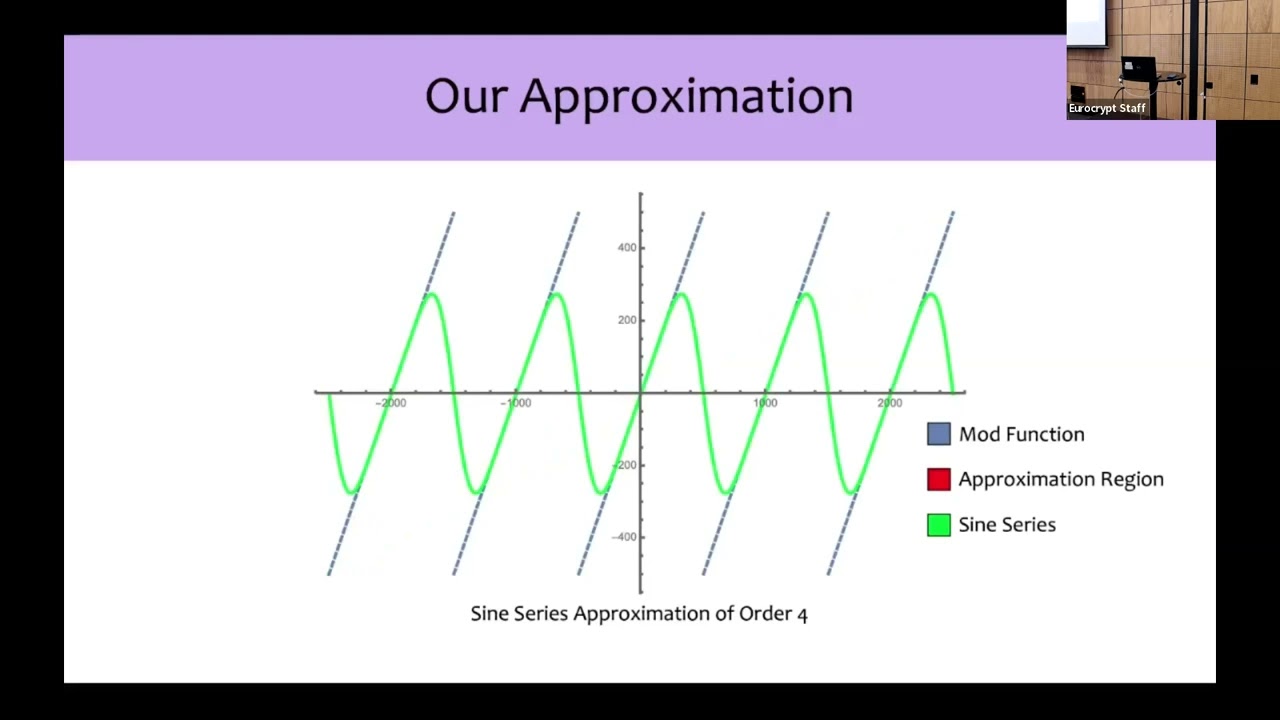
Abstract:While it is well known that the sawtooth function has a point-wise convergent Fourier series, the rate of convergence is not the best possible for the application of approximating the mod function in small intervals around multiples of the modulus. We show a different sine series, such that the sine series of order n has error O(epsilon^(2n+1)) for approximating the mod function in epsilon-sized intervals around multiples of the modulus. Moreover, the resulting polynomial, after Taylor series approximation of the sine series, has small coefficients, and the whole polynomial can be computed at a precision that is only slightly larger than -(2n+1)log epsilon, the precision of approximation being sought. This polynomial can then be used to approximate the mod function to almost arbitrary precision, and hence allows practical CKKS-HE bootstrapping with arbitrary precision. We validate our approach with an implementation and obtain 100 bit precision bootstrapping as well as improvements over earlier works at lower precision.
ePrint: https://eprint.iacr.org/2021/572
Talk: https://www.youtube.com/watch?v=hd5CV4b2hYU
Slides: https://iacr.org/submit/files/slides/2022/eurocrypt/eurocrypt2022/214/slides.pptx
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .