Welcome to the resource topic for 2021/535
Title:
On the Possibility of Basing Cryptography on \EXP \neq \BPP
Authors: Yanyi Liu, Rafael Pass
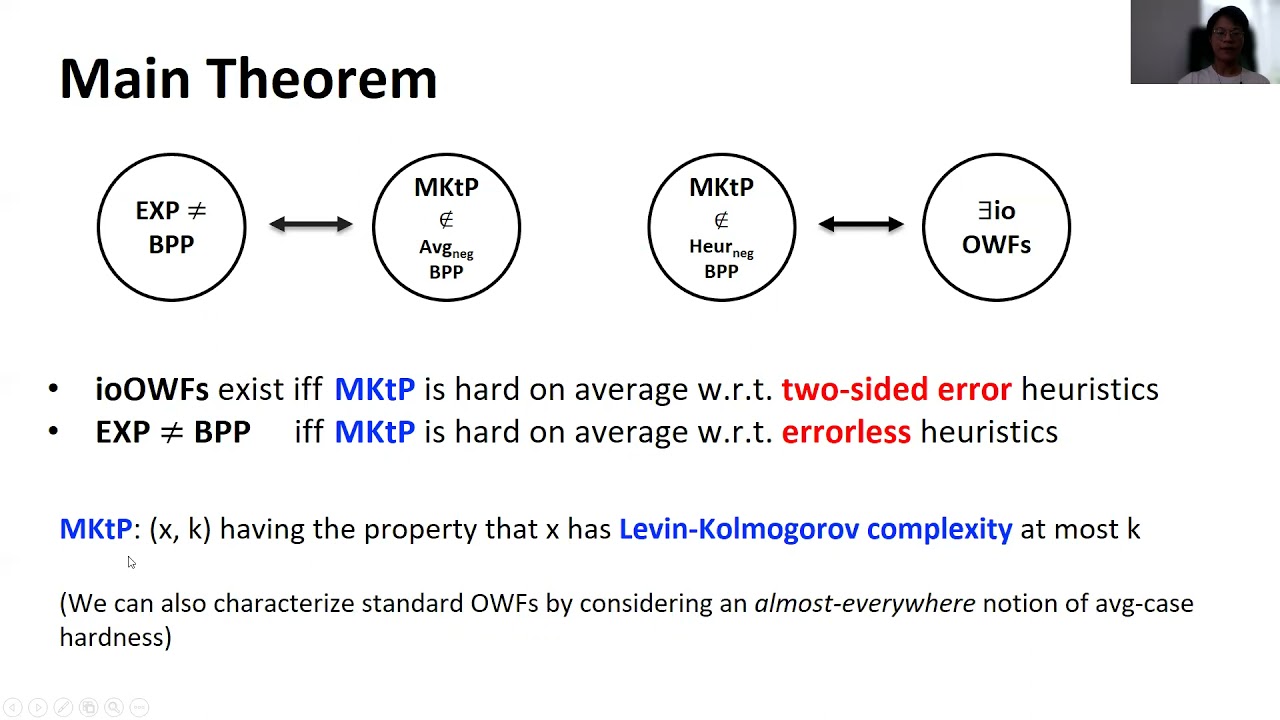
Abstract:Liu and Pass (FOCS’20) recently demonstrated an equivalence between the existence of one-way functions (OWFs) and mild average-case hardness of the time-bounded Kolmogorov complexity problem. In this work, we establish a similar equivalence but to a different form of time-bounded Kolmogorov Complexity—namely, Levin’s notion of Kolmogorov Complexity—whose hardness is closely related to the problem of whether \EXP \neq \BPP. In more detail, let Kt(x) denote the Levin-Kolmogorov Complexity of the string x; that is, Kt(x) = \min_{\desc \in \bitset^*, t \in \N}\{|\desc| + \lceil \log t \rceil: U(\desc, 1^t) = x\}, where U is a universal Turing machine, and U(\desc,1^t) denotes the output of the program \Pi after t steps, and let \mktp denote the language of pairs (x,k) having the property that Kt(x) \leq k. We demonstrate that: - \mktp \notin \HeurpBPP (i.e., \mktp is infinitely-often \emph{two-sided error} mildly average-case hard) iff infinititely-often OWFs exist. - \mktp \notin \AvgpBPP (i.e., \mktp is infinitely-often \emph{errorless} mildly average-case hard) iff \EXP \neq \BPP. Thus, the only gap'' towards getting (infinitely-often) OWFs from the assumption that $\EXP \neq \BPP$ is the seemingly minor’’ technical gap between two-sided error and errorless average-case hardness of the \mktp problem. As a corollary of this result, we additionally demonstrate that any reduction from errorless to two-sided error average-case hardness for \mktp implies (unconditionally) that \NP \neq \P. We finally consider other alternative notions of Kolmogorov complexity—including space-bounded Kolmogorov complexity and conditional Kolmogorov complexity—and show how average-case hardness of problems related to them characterize log-space computable OWFs, or OWFs in \NC^0.
ePrint: https://eprint.iacr.org/2021/535
Talk: https://www.youtube.com/watch?v=nBDzPqHzu4o
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .