Welcome to the resource topic for 2021/507
Title:
The t-wise Independence of Substitution-Permutation Networks
Authors: Tianren Liu, Stefano Tessaro, Vinod Vaikuntanathan
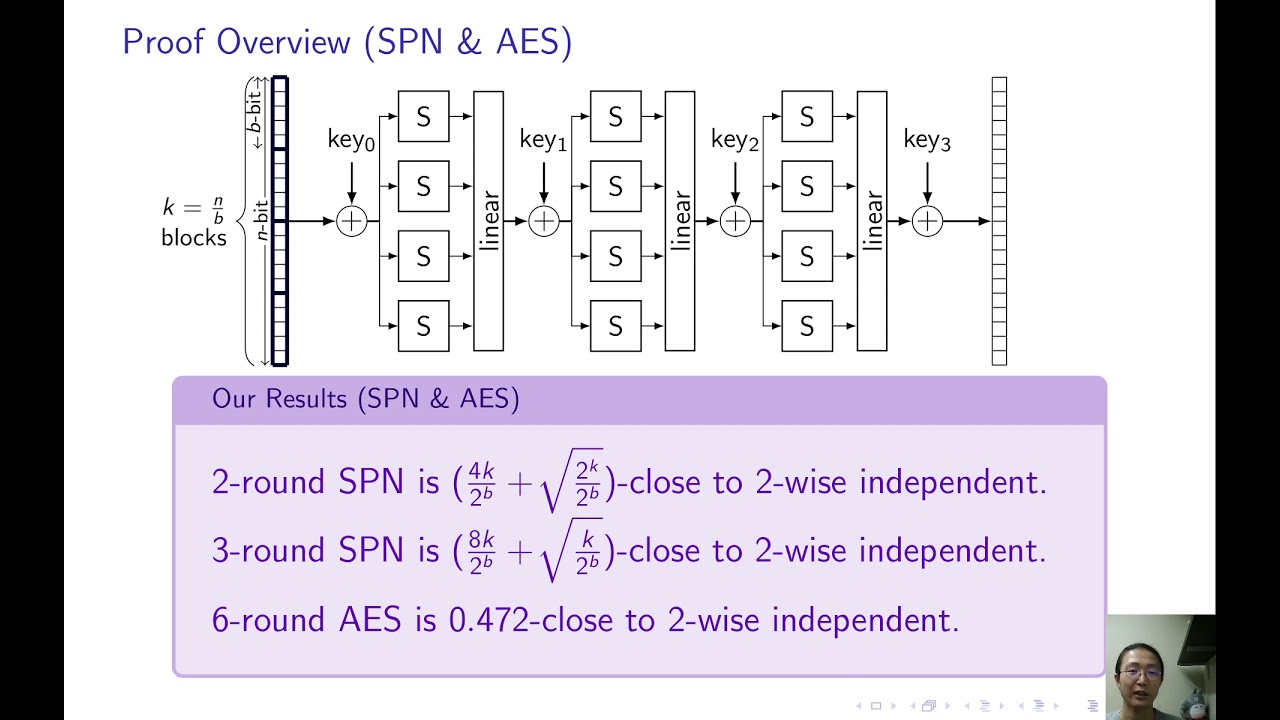
Abstract:Block ciphers such as the Advanced Encryption Standard (Rijndael) are used extensively in practice, yet our understanding of their security continues to be highly incomplete. This paper promotes and continues a research program aimed at proving the security of block ciphers against important and well-studied classes of attacks. In particular, we initiate the study of (almost) t-wise independence of concrete block-cipher construction paradigms such as substitution-permutation networks and key-alternating ciphers. Sufficiently strong (almost) pairwise independence already suffices to resist (truncated) differential attacks and linear cryptanalysis, and hence this is a relevant and meaningful target. Our results are two-fold. Our first result concerns substitution-permutation networks (SPNs) that model ciphers such as AES. We prove the almost pairwise-independence of an SPN instantiated with concrete S-boxes together with an appropriate linear mixing layer, given sufficiently many rounds and independent sub-keys. Our proof relies on a characterization of S-box computation on input differences in terms of sampling output differences from certain subspaces, and a new randomness extraction lemma (which we prove with Fourier-analytic techniques) that establishes when such sampling yields uniformity. We use our techniques in particular to prove almost pairwise-independence for sufficiently many rounds of both the AES block cipher (which uses a variant of the patched inverse function x \mapsto x^{-1} as the S-box) and the MiMC block cipher (which uses the cubing function x \mapsto x^3 as the S-box), assuming independent sub-keys. Secondly, we show that instantiating a key-alternating cipher (which can be thought of as a degenerate case of SPNs) with most permutations gives us (almost) t-wise independence in t + o(t) rounds. In order to do this, we use the probabilistic method to develop two new lemmas, an independence-amplification lemma and a distance amplification lemma, that allow us to reason about the evolution of key-alternating ciphers.
ePrint: https://eprint.iacr.org/2021/507
Talk: https://www.youtube.com/watch?v=6cd8XzlXXJ8
Slides: https://iacr.org/submit/files/slides/2021/crypto/crypto2021/375/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .