Welcome to the resource topic for 2021/1464
Title:
Polynomial-time targeted attacks on coin tossing for any number of corruptions
Authors: Omid Etesami, Ji Gao, Saeed Mahloujifar, Mohammad Mahmoody
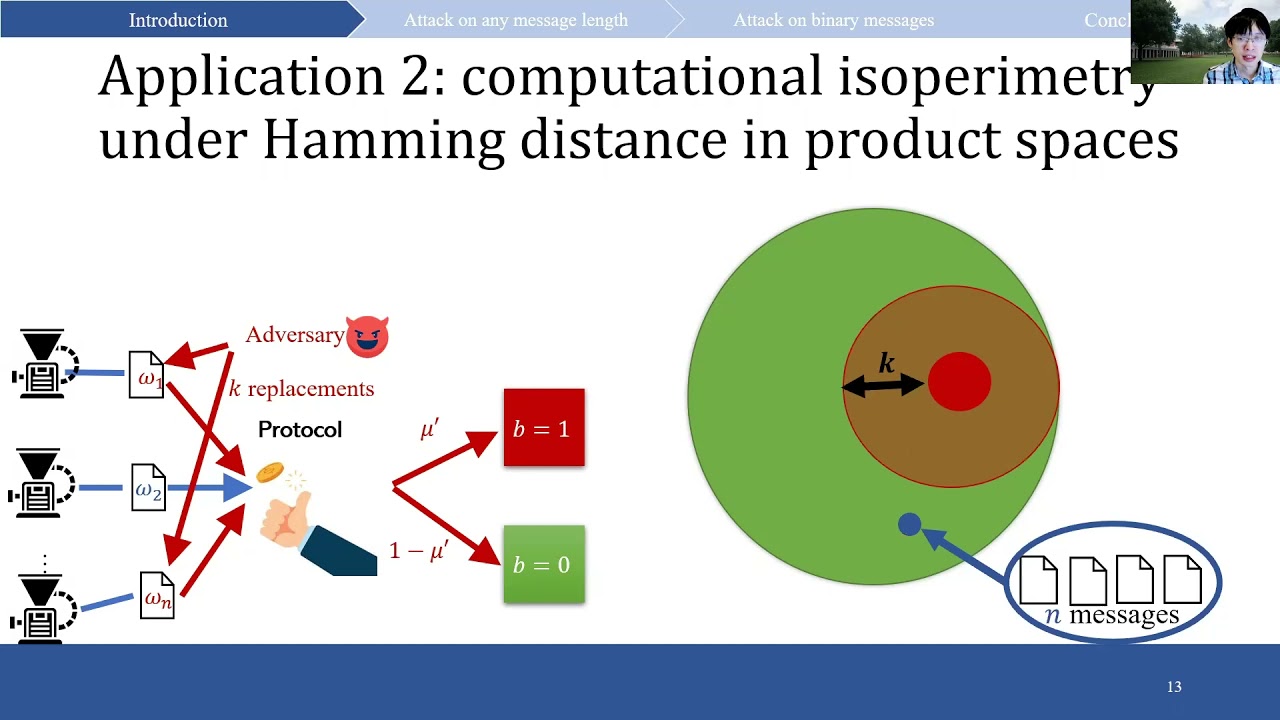
Abstract:Consider an n-message coin-tossing protocol between n parties P_1,\dots,P_n, in which P_i broadcasts a single message w_i in round i (possibly based on the previously shared messages) and at the end they agree on bit b. A k-replacing adversary A_k can change up to k of the messages as follows. In every round i, the adversary who knows all the messages broadcast so far, as well as a message w_i that is prepared by P_i to be just sent, can can to replace the prepared message w_i with its own choice. A targeted adversary prefers the outcome b'=1, and its bias is defined as \mu'-\mu, where \mu'=\Pr[b'=1] (resp. \Pr[b=1]=\mu) refers to the probability of outputting 1 when the attack happens (resp. does not happen). In this work, we study k-replacing targeted attacks, their computational efficiency, and optimality, for all k \in [n]. Large messages: When the messages are allowed to be arbitrarily long, we show that polynomial-time k-replacing targeted attacks can achieve bias \Omega(\mu k/\sqrt n) for any k (and any protocol), which is optimal up to a constant factor for any \mu = \Theta(1). Previously, it was known how to achieve such bias only for k = \Omega(\sqrt n) (Komargodski-Raz [DISC’18], Mahloujifar-Mahmoody [ALT’19], and Etesami-Mahloujifar-Mahmoody [SODA’20]). This proves a computational variant of the isoperimetric inequality for product spaces under k=o(\sqrt n) Hamming distance. As a corollary, we also obtain improved poly(n)-time targeted poisoning attacks on deterministic learners, in which the adversary can increase the probability of any efficiently testable bad event over the produced model from \mu=1/poly(n) to \mu + \Omega(\mu k /\sqrt n) by changing k out of n training examples. Binary messages: When the messages w_1,\dots,w_n are uniformly random bits, we show that if \mu=\Pr[b=1]= \Pr[\sum w_i \geq t] = \beta^{(t)}_n for t \in [n] is the probability of falling into a Hamming ball, then polynomial-time k-replacing targeted attacks can achieve \mu'=\Pr[b'=1]=\beta^{(t-k)}_n , which is optimal due to the simple majority protocol. Thus, as corollary we obtain an alternative proof of the Harper’s celebrated vertex isoperimetric inequality in which the optimal adversary (that maps random points to a set of measure \mu by changing at most k bits) is limited to be online and run in polynomial time. Previously, Lichtenstein, Linial, and Saks [Combinatorica’89] showed how to achieve \mu'=\Pr[b'=1] = \beta^{(t-k)}_{ n-k } (using computationally unbounded attacks), which is optimal for adaptive adversaries who decide on corrupting parties before seeing their messages.
ePrint: https://eprint.iacr.org/2021/1464
Talk: https://www.youtube.com/watch?v=iZkAq4htW-c
Slides: https://iacr.org/submit/files/slides/2021/tcc/tcc2021/246/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .