Welcome to the resource topic for 2021/1220
Title:
Digital Signatures with Memory-Tight Security in the Multi-Challenge Setting
Authors: Denis Diemert, Kai Gellert, Tibor Jager, Lin Lyu
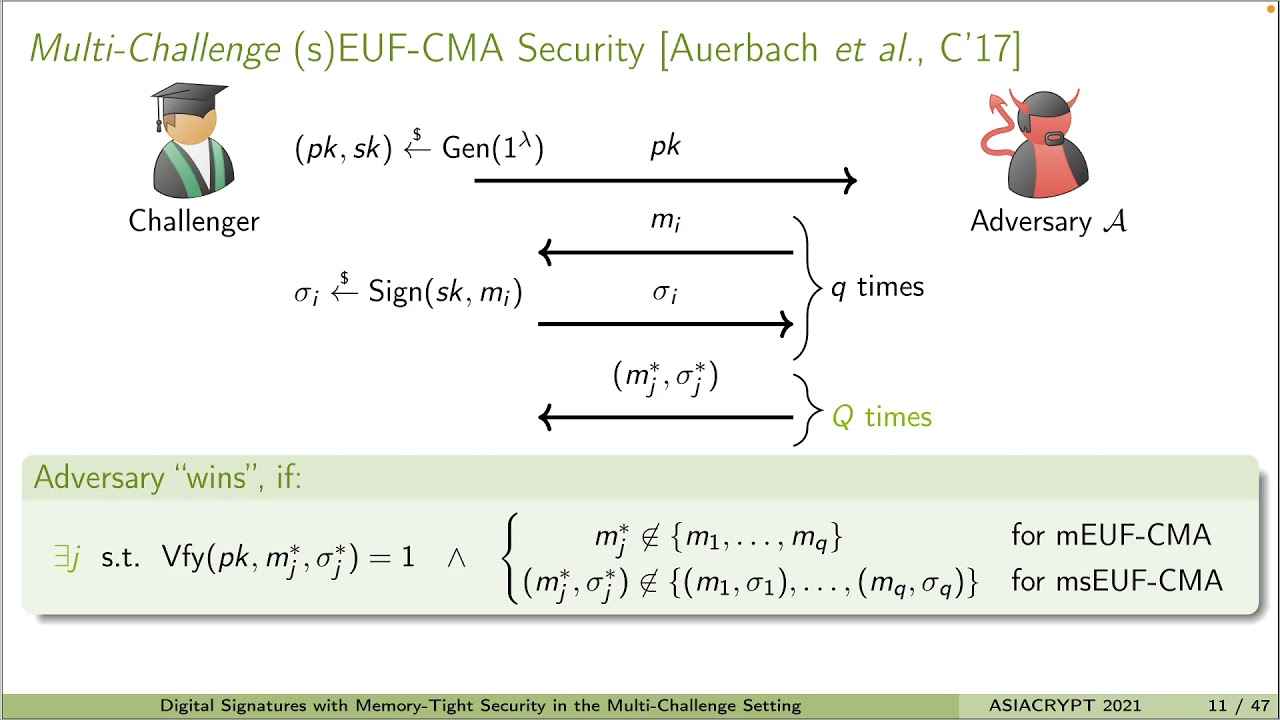
Abstract:The standard security notion for digital signatures is “single-challenge” (SC) EUF-CMA security, where the adversary outputs a single message-signature pair and “wins” if it is a forgery. Auerbach et al. (CRYPTO 2017) introduced memory-tightness of reductions and argued that the right security goal in this setting is actually a stronger “multi-challenge” (MC) definition, where an adversary may output many message-signature pairs and “wins” if at least one is a forgery. Currently, no construction from simple standard assumptions is known to achieve full tightness with respect to time, success probability, and memory simultaneously. Previous works showed that memory-tight signatures cannot be achieved via certain natural classes of reductions (Auerbach et al., CRYPTO 2017; Wang et al., EUROCRYPT 2018). These impossibility results may give the impression that the construction of memory-tight signatures is difficult or even impossible. We show that this impression is false, by giving the first constructions of signature schemes with full tightness in all dimensions in the MC setting. To circumvent the known impossibility results, we first introduce the notion of canonical reductions in the SC setting. We prove a general theorem establishing that every signature scheme with a canonical reduction is already memory-tightly secure in the MC setting, provided that it is strongly unforgeable, the adversary receives only one signature per message, and assuming the existence of a tightly-secure pseudorandom function. We then achieve memory-tight many-signatures-per-message security in the MC setting by a simple additional generic transformation. This yields the first memory-tightly, strongly EUF-CMA-secure signature schemes in the MC setting. Finally, we show that standard security proofs often already can be viewed as canonical reductions. Concretely, we show this for signatures from lossy identification schemes (Abdalla et al., EUROCRYPT 2012), two variants of RSA Full-Domain Hash (Bellare and Rogaway, EUROCRYPT 1996), and two variants of BLS signatures (Boneh et al., ASIACRYPT 2001).
ePrint: https://eprint.iacr.org/2021/1220
Talk: https://www.youtube.com/watch?v=CXPu7e13ga8
Slides: https://iacr.org/submit/files/slides/2021/asiacrypt/asiacrypt2021/147/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .