Welcome to the resource topic for 2020/768
Title:
Perfect Zero Knowledge: New Upperbounds and Relativized Separations
Authors: Peter Dixon, Sutanu Gayen, A. Pavan, N. V. Vinodchandran
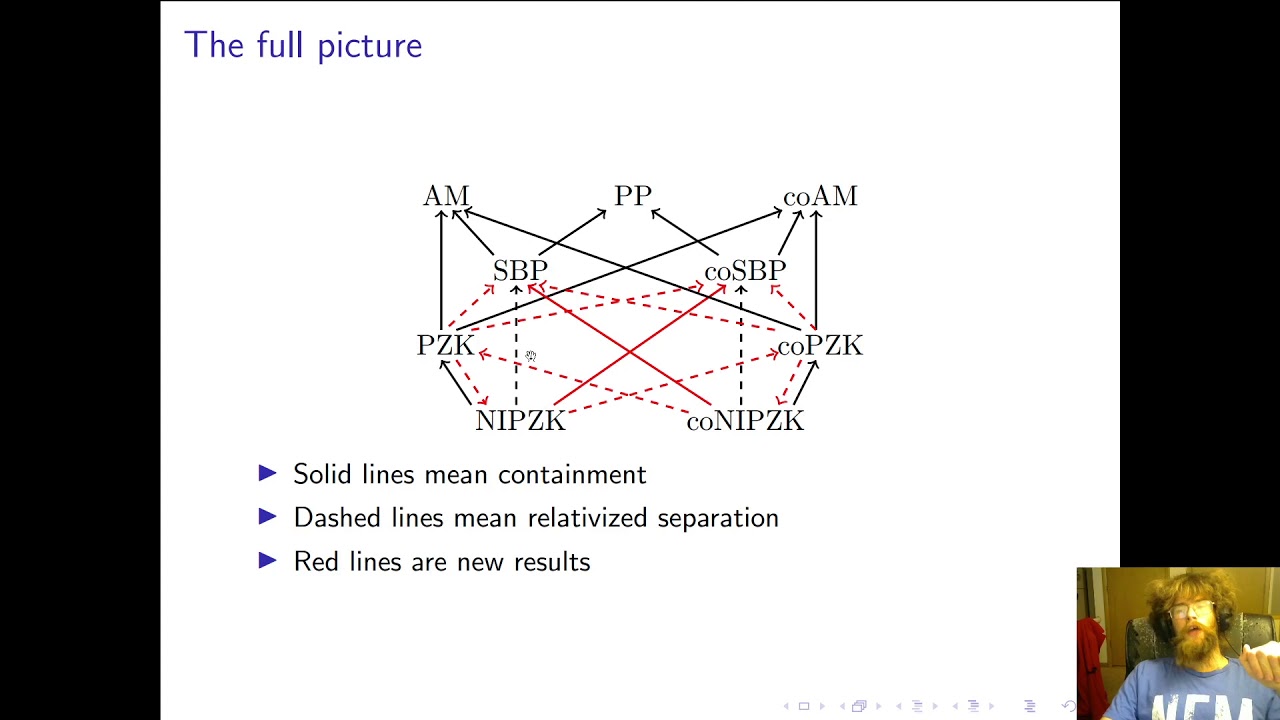
Abstract:We investigate the complexity of problems that admit perfect zero-knowledge interactive protocols and establish new unconditional upper bounds and oracle separation results. We establish our results by investigating certain distribution testing problems: computational problems over high-dimensional distributions represented by succinct Boolean circuits. A relatively less-investigated complexity class SBP emerged as significant in this study. The main results we establish are: 1. A unconditional inclusion that NIPZK is in CoSBP. 2. Construction of a relativized world in which there is a distribution testing problem that lies in NIPZK but not in SBP, thus giving a relativized separation of NIPZK (and hence PZK) from SBP. 3. Construction of a relativized world in which there is a distribution testing problem that lies in PZK but not in CoSBP, thus giving a relativized separation of PZK from CoSBP. These results refine the landscape of perfect zero-knowledge classes in relation to traditional complexity classes.
ePrint: https://eprint.iacr.org/2020/768
Talk: https://www.youtube.com/watch?v=cjTBVRtJIVg
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .