Welcome to the resource topic for 2020/762
Title:
Functional Encryption for Attribute-Weighted Sums from k-Lin
Authors: Michel Abdalla, Junqing Gong, Hoeteck Wee
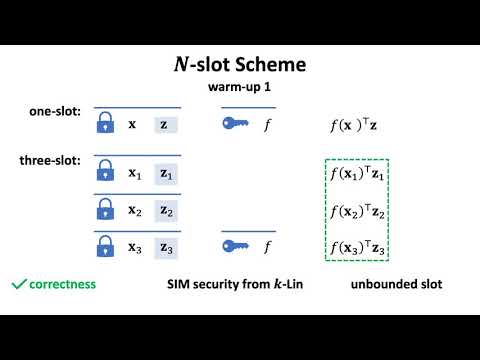
Abstract:We present functional encryption schemes for attribute-weighted sums, where encryption takes as input N attribute-value pairs (x_i,z_i) where x_i is public and z_i is private; secret keys are associated with arithmetic branching programs f, and decryption returns the weighted sum \sum_{i=1}^N f(x_i) z_i while leaking no additional information about the z_i's. Our main construction achieves (1) compact public parameters and key sizes that are independent of N and the secret key can decrypt a ciphertext for any a-prior unbounded N; (2) short ciphertexts that grow with N and the size of z_i but not x_i; (3) simulation-based security against unbounded collusions; (4) relies on the standard k-linear assumption in prime-order bilinear groups.
ePrint: https://eprint.iacr.org/2020/762
Talk: https://www.youtube.com/watch?v=dMHXu0MCz80
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .