Welcome to the resource topic for 2020/256
Title:
Statistical ZAPR Arguments from Bilinear Maps
Authors: Alex Lombardi, Vinod Vaikuntanathan, Daniel Wichs
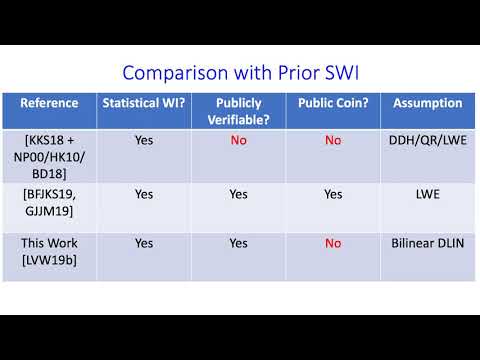
Abstract:Dwork and Naor (FOCS ‘00) defined ZAPs as 2-message witness-indistinguishable proofs that are public-coin. We relax this to ZAPs with private randomness'' (ZAPRs), where the verifier can use private coins to sample the first message (independently of the statement being proved), but the proof must remain publicly verifiable given only the protocol transcript. In particular, ZAPRs are reusable, meaning that the first message can be reused for multiple proofs without compromising security. Known constructions of ZAPs from trapdoor permutations or bilinear maps are only computationally WI (and statistically sound). Two recent results of Badrinarayanan-Fernando-Jain-Khurana-Sahai and Goyal-Jain-Jin-Malavolta [EUROCRYPT '20] construct the first statistical ZAP arguments, which are statistically WI (and computationally sound), from the quasi-polynomial LWE assumption. Here, we construct statistical ZAPR arguments from the quasi-polynomial decision-linear (DLIN) assumption on groups with a bilinear map. Our construction relies on a combination of several tools, including the Groth-Ostrovsky-Sahai NIZK and NIWI [EUROCRYPT '06, CRYPTO '06, JACM '12], sometimes-binding statistically hiding commitments’’ [Kalai-Khurana-Sahai, EUROCRYPT ‘18] and the ``MPC-in-the-head’’ technique [Ishai-Kushilevitz-Ostrovsky-Sahai, STOC '07].
ePrint: https://eprint.iacr.org/2020/256
Talk: https://www.youtube.com/watch?v=pAlNT8VPRlc
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .