Welcome to the resource topic for 2020/1527
Title:
Zero-Knowledge IOPs with Linear-Time Prover and Polylogarithmic-Time Verifier
Authors: Jonathan Bootle, Alessandro Chiesa, and Siqi Liu
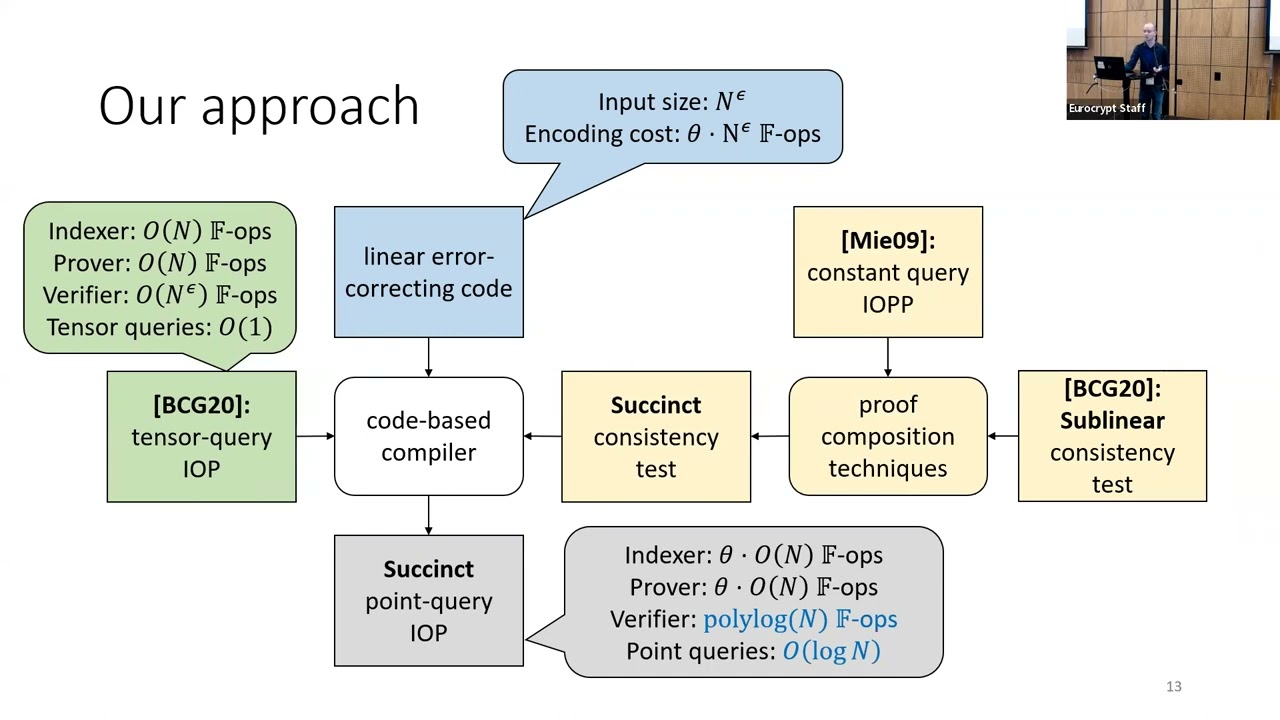
Abstract:Interactive oracle proofs (IOPs) are a multi-round generalization of probabilistically checkable proofs that play a fundamental role in the construction of efficient cryptographic proofs. We present an IOP that simultaneously achieves the properties of zero knowledge, linear-time proving, and polylogarithmic-time verification. We construct a zero-knowledge IOP where, for the satisfiability of an N-gate arithmetic circuit over any field of size \Omega(N), the prover uses O(N) field operations and the verifier uses \polylog(N) field operations (with proof length O(N) and query complexity \polylog(N)). Polylogarithmic verification is achieved in the holographic setting for every circuit (the verifier has oracle access to a linear-time-computable encoding of the circuit whose satisfiability is being proved). Our result implies progress on a basic goal in the area of efficient zero knowledge. Via a known transformation, we obtain a zero knowledge argument system where the prover runs in linear time and the verifier runs in polylogarithmic time; the construction is plausibly post-quantum and only makes a black-box use of lightweight cryptography (collision-resistant hash functions).
ePrint: https://eprint.iacr.org/2020/1527
Talk: https://www.youtube.com/watch?v=3AGLkyIPWBc
Slides: https://iacr.org/submit/files/slides/2022/eurocrypt/eurocrypt2022/101/slides.pptx
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .