Welcome to the resource topic for 2020/1510
Title:
Quantum Computationally Predicate-Binding Commitments with Application in Quantum Zero-Knowledge Arguments for NP
Authors: Jun Yan
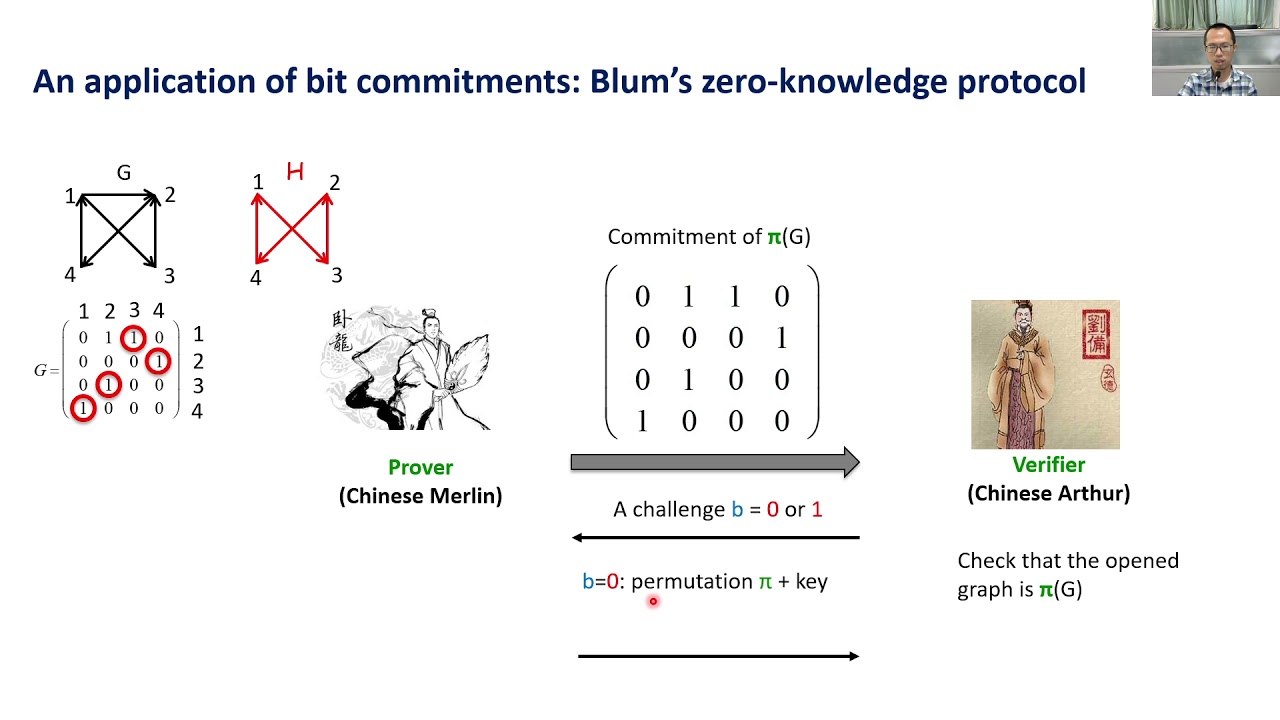
Abstract:A quantum bit commitment scheme is to realize bit (rather than qubit) commitment by exploiting quantum communication and quantum computation. In this work, we study the binding property of the quantum string commitment scheme obtained by composing a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme (which can be realized based on quantum-secure one-way permutations(resp. functions)) in parallel. We show that the resulting scheme satisfies a stronger quantum computational binding property, which we will call predicate-binding, than the trivial honest-binding. Intuitively and very roughly, the predicate-binding property guarantees that given any inconsistent predicate pair over a set of strings (i.e. no strings in this set can satisfy both predicates), if a (claimed) quantum commitment can be opened so that the revealed string satisfies one predicate with certainty, then the same commitment cannot be opened so that the revealed string satisfies the other predicate (except for a negligible probability). As an application, we plug a generic quantum perfectly(resp. statistically)-hiding computationally-binding bit commitment scheme in Blum’s zero-knowledge protocol for the NP-complete language Hamiltonian Cycle. The quantum computational soundness of the resulting protocol will follow immediately from the quantum computational predicate-binding property of commitments. Combined with the perfect(resp. statistical) zero-knowledge property which can be similarly established as in previous work, this gives rise to the first quantum perfect(resp. statistical) zero-knowledge argument system (with soundness error 1/2) for all NP languages based solely on quantum-secure one-way permutations(resp. functions).
ePrint: https://eprint.iacr.org/2020/1510
Talk: https://www.youtube.com/watch?v=jMvjzbJqPRo
Slides: https://iacr.org/submit/files/slides/2021/asiacrypt/asiacrypt2021/199/slides.pptx
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .