Welcome to the resource topic for 2020/1508
Title:
A Combinatorial Approach to Quantum Random Functions
Authors: Nico Döttling, Giulio Malavolta, Sihang Pu
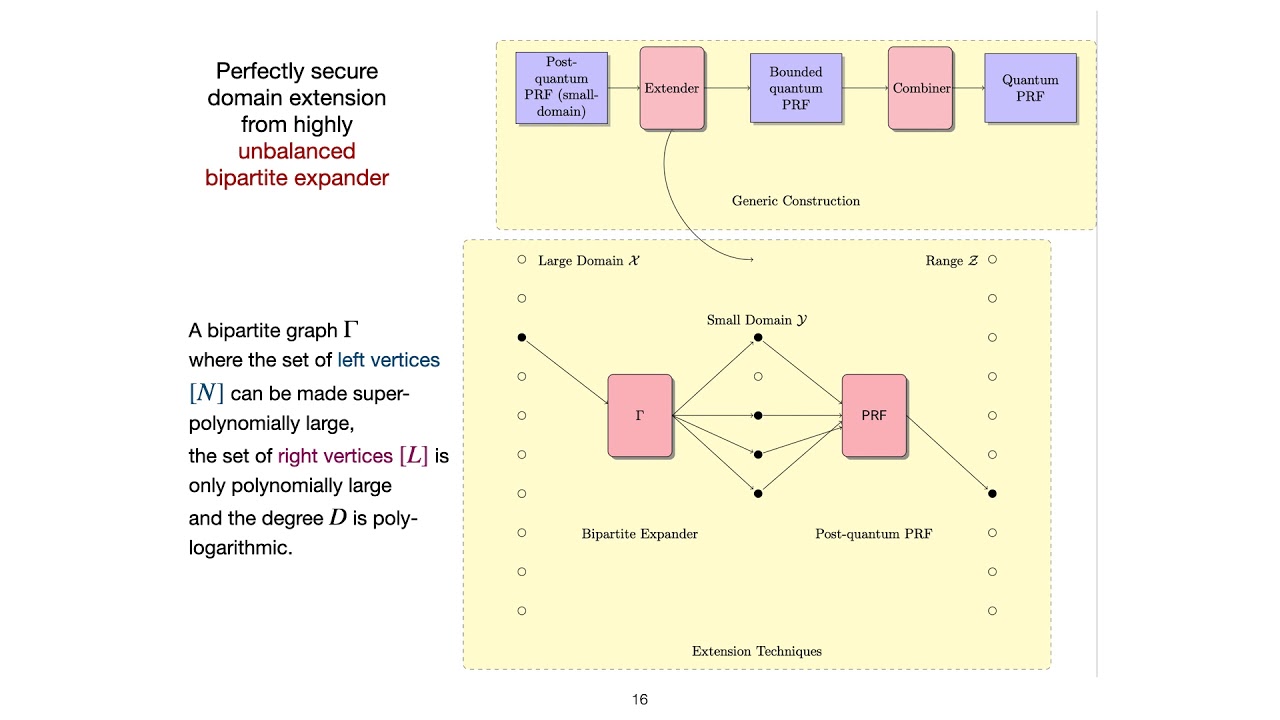
Abstract:Quantum pseudorandom functions (QPRFs) extend the classical security of a PRF by allowing the adversary to issue queries on input superposition. Zhandry [Zhandry, FOCS 2012] showed a separation between the two notions and proved that common construction paradigms are also quantum secure, albeit with a new ad-hoc analysis. In this work, we revisit the question of constructing QPRFs and propose a new method starting from small-domain (classical) PRFs: At the heart of our approach is a new domain-extension technique based on bipartite expanders. Interestingly, our analysis is almost entirely classical. As a corollary of our main theorem, we obtain the first (approximate) key homomorphic quantum PRF based on the quantum intractability of the learning with errors problem.
ePrint: https://eprint.iacr.org/2020/1508
Talk: https://www.youtube.com/watch?v=mr2vNeLg28I
Slides: https://iacr.org/submit/files/slides/2020/asiacrypt/ac2020/293/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .