Welcome to the resource topic for 2020/1451
Title:
Efficient Fully Secure Computation via Distributed Zero-Knowledge Proofs
Authors: Elette Boyle, Niv Gilboa, Yuval Ishai, Ariel Nof
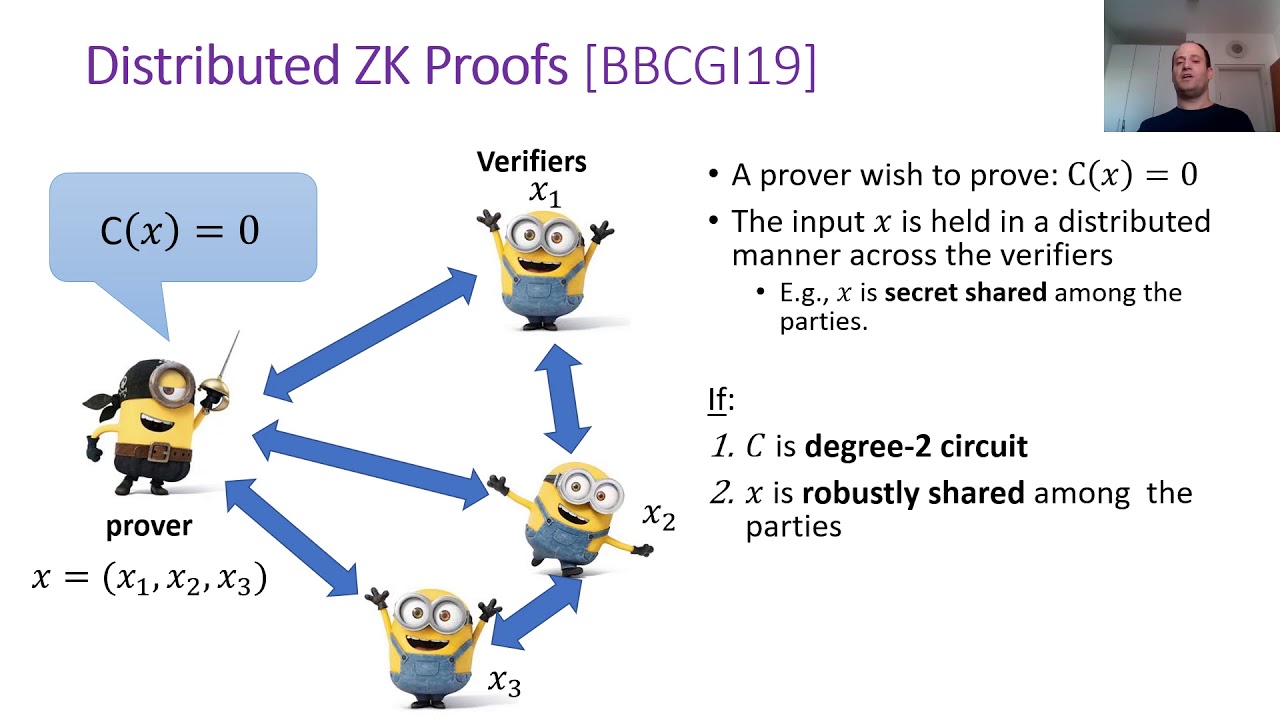
Abstract:Secure computation protocols enable mutually distrusting parties to compute a function of their private inputs while revealing nothing but the output. Protocols with {\em full security} (also known as {\em guaranteed output delivery}) in particular protect against denial-of-service attacks, guaranteeing that honest parties receive a correct output. This feature can be realized in the presence of an honest majority, and significant research effort has gone toward attaining full security with good asymptotic and concrete efficiency. We present an efficient protocol for {\em any constant} number of parties n, with {\em full security} against t<n/2 corrupted parties, that makes a black-box use of a pseudorandom generator. Our protocol evaluates an arithmetic circuit C over a finite ring R (either a finite field or R=\Z_{2^k}) with communication complexity of \frac{3t}{2t+1}S + o(S) R-elements per party, where S is the number of multiplication gates in C (namely, <1.5 elements per party per gate). This matches the best known protocols for the semi-honest model up to the sublinear additive term. For a small number of parties n, this improves over a recent protocol of Goyal {\em et al.} (Crypto 2020) by a constant factor for circuits over large fields, and by at least an \Omega(\log n) factor for Boolean circuits or circuits over rings. Our protocol provides new methods for applying the sublinear-communication distributed zero-knowledge proofs of Boneh {\em et al.}~(Crypto 2019) for compiling semi-honest protocols into fully secure ones, in the more challenging case of t>1 corrupted parties. Our protocol relies on {\em replicated secret sharing} to minimize communication and simplify the mechanism for achieving full security. This results in computational cost that scales exponentially with n. Our main fully secure protocol builds on a new intermediate honest-majority protocol for verifying the correctness of multiplication triples by making a {\em general} use of distributed zero-knowledge proofs. While this intermediate protocol only achieves the weaker notion of {\em security with abort}, it applies to any linear secret-sharing scheme and provides a conceptually simpler, more general, and more efficient alternative to previous protocols from the literature. In particular, it can be combined with the Fiat-Shamir heuristic to simultaneously achieve logarithmic communication complexity and constant round complexity.
ePrint: https://eprint.iacr.org/2020/1451
Talk: https://www.youtube.com/watch?v=kA6J5wAQZMo
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .