Welcome to the resource topic for 2020/1182
Title:
On the Round Complexity of the Shuffle Model
Authors: Amos Beimel, Iftach Haitner, Kobbi Nissim, Uri Stemmer
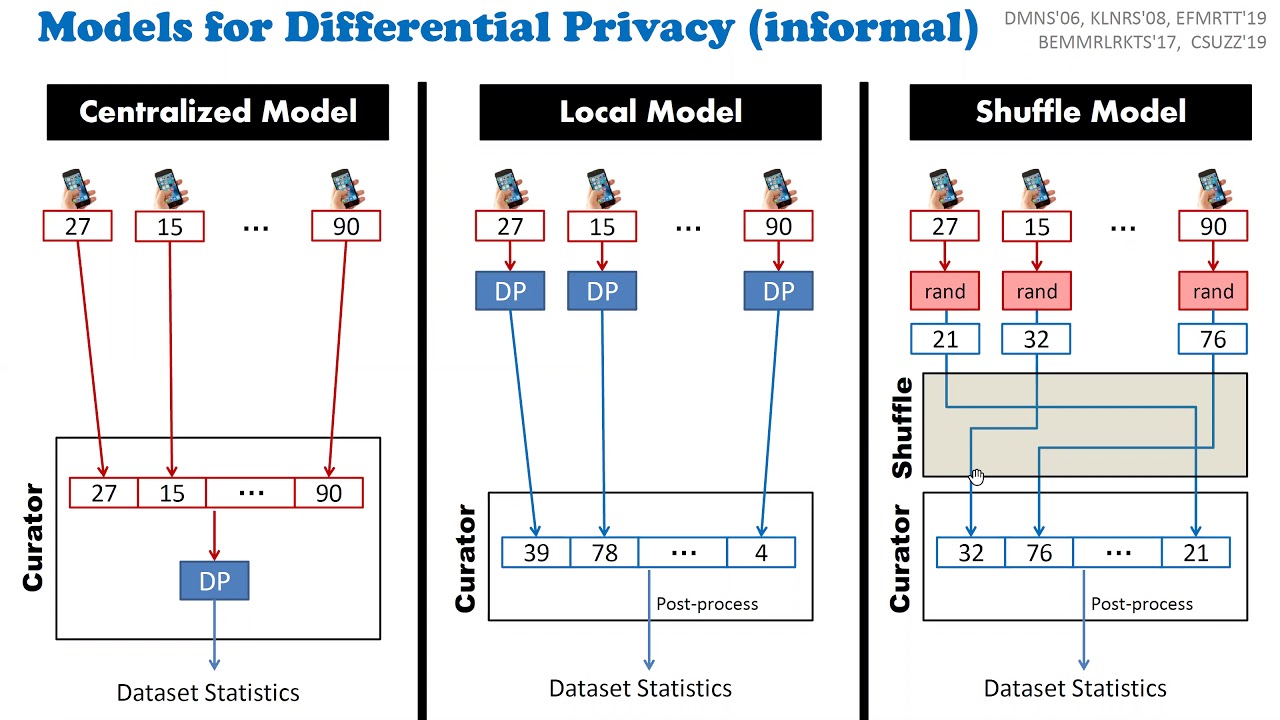
Abstract:The shuffle model of differential privacy [Bittau et al. SOSP 2017; Erlingsson et al. SODA 2019; Cheu et al. EUROCRYPT 2019] was proposed as a viable model for performing distributed differentially private computations. Informally, the model consists of an untrusted analyzer that receives messages sent by participating parties via a shuffle functionality, the latter potentially disassociates messages from their senders. Prior work focused on one-round differentially private shuffle model protocols, demonstrating that functionalities such as addition and histograms can be performed in this model with accuracy levels similar to that of the curator model of differential privacy, where the computation is performed by a fully trusted party. A model closely related to the shuffle model was presented in the seminal work of Ishai et al. on establishing cryptography from anonymous communication [FOCS 2006]. Focusing on the round complexity of the shuffle model, we ask in this work what can be computed in the shuffle model of differential privacy with two rounds. Ishai et al. showed how to use one round of the shuffle to establish secret keys between every two parties. Using this primitive to simulate a general secure multi-party protocol increases its round complexity by one. We show how two parties can use one round of the shuffle to send secret messages without having to first establish a secret key, hence retaining round complexity. Combining this primitive with the two-round semi-honest protocol of Applebaum, Brakerski, and Tsabary [TCC 2018], we obtain that every randomized functionality can be computed in the shuffle model with an honest majority, in merely two rounds. This includes any differentially private computation. We hence move to examine differentially private computations in the shuffle model that (i) do not require the assumption of an honest majority, or (ii) do not admit one-round protocols, even with an honest majority. For that, we introduce two computational tasks: common element, and nested common element with parameter \alpha. For the common element problem we show that for large enough input domains, no one-round differentially private shuffle protocol exists with constant message complexity and negligible \delta, whereas a two-round protocol exists where every party sends a single message in every round. For the nested common element we show that no one-round differentially private protocol exists for this problem with adversarial coalition size \alpha n. However, we show that it can be privately computed in two rounds against coalitions of size cn for every c < 1. This yields a separation between one-round and two-round protocols. We further show a one-round protocol for the nested common element problem that is differentially private with coalitions of size smaller than c n for all 0 < c < \alpha < 1 / 2.
ePrint: https://eprint.iacr.org/2020/1182
Talk: https://www.youtube.com/watch?v=FkKbjgJ_RBs
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .