Welcome to the resource topic for 2020/1167
Title:
Batch Verification for Statistical Zero Knowledge Proofs
Authors: Inbar Kaslasi, Guy N. Rothblum, Ron D. Rothblum, Adam Sealfon, Prashant Nalini Vasudevan
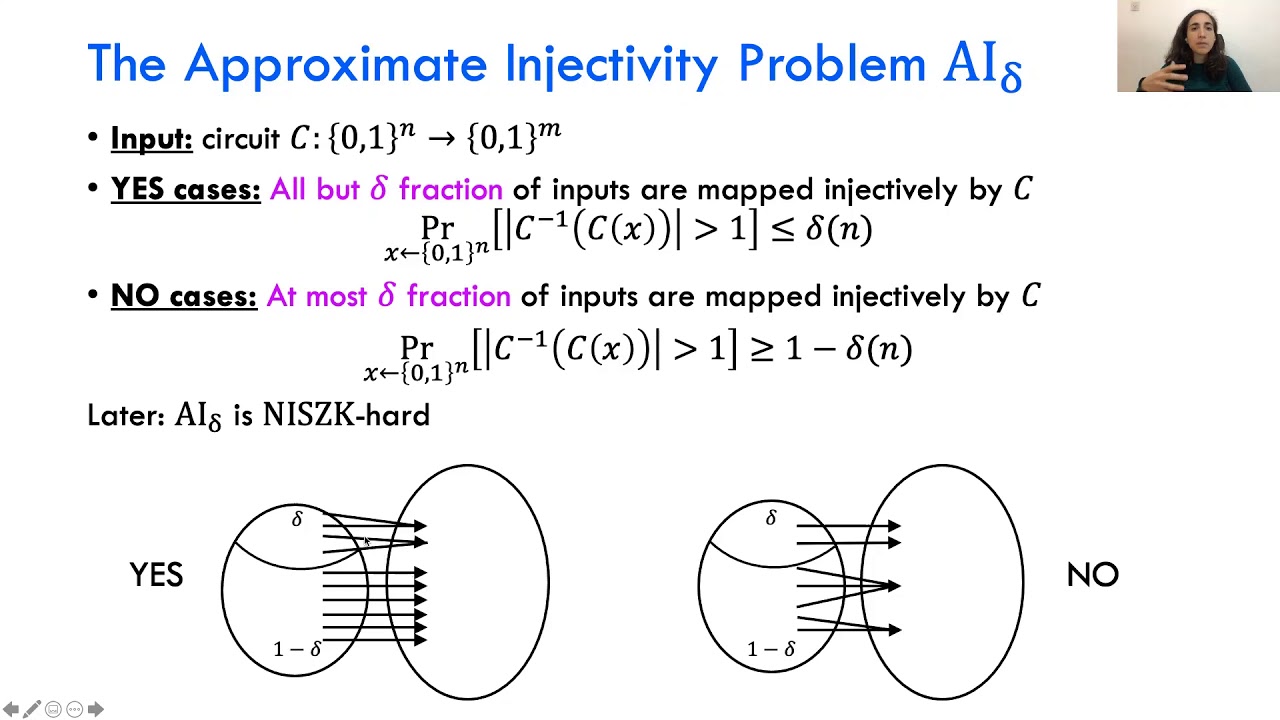
Abstract:A statistical zero-knowledge proof (SZK) for a problem \Pi enables a computationally unbounded prover to convince a polynomial-time verifier that x \in \Pi without revealing any additional information about x to the verifier, in a strong information-theoretic sense. Suppose, however, that the prover wishes to convince the verifier that k separate inputs x_1,\dots,x_k all belong to \Pi (without revealing anything else). A naive way of doing so is to simply run the SZK protocol separately for each input. In this work we ask whether one can do better – that is, is efficient batch verification possible for SZK? We give a partial positive answer to this question by constructing a batch verification protocol for a natural and important subclass of SZK – all problems \Pi that have a non-interactive SZK protocol (in the common random string model). More specifically, we show that, for every such problem \Pi, there exists an honest-verifier SZK protocol for batch verification of k instances, with communication complexity poly(n) + k \cdot poly(\log{n},\log{k}), where poly refers to a fixed polynomial that depends only on \Pi (and not on k). This result should be contrasted with the naive solution, which has communication complexity k \cdot poly(n). Our proof leverages a new NISZK-complete problem, called Approximate Injectivity, that we find to be of independent interest. The goal in this problem is to distinguish circuits that are nearly injective, from those that are non-injective on almost all inputs.
ePrint: https://eprint.iacr.org/2020/1167
Talk: https://www.youtube.com/watch?v=L8ETmxEhXHk
Slides: https://iacr.org/submit/files/slides/2020/tcc/tcc2020/147/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .