Welcome to the resource topic for 2020/1025
Title:
A Bit-Vector Differential Model for the Modular Addition by a Constant
Authors: Seyyed Arash Azimi, Adrián Ranea, Mahmoud Salmasizadeh, Javad Mohajeri, Mohammad Reza Aref, Vincent Rijmen
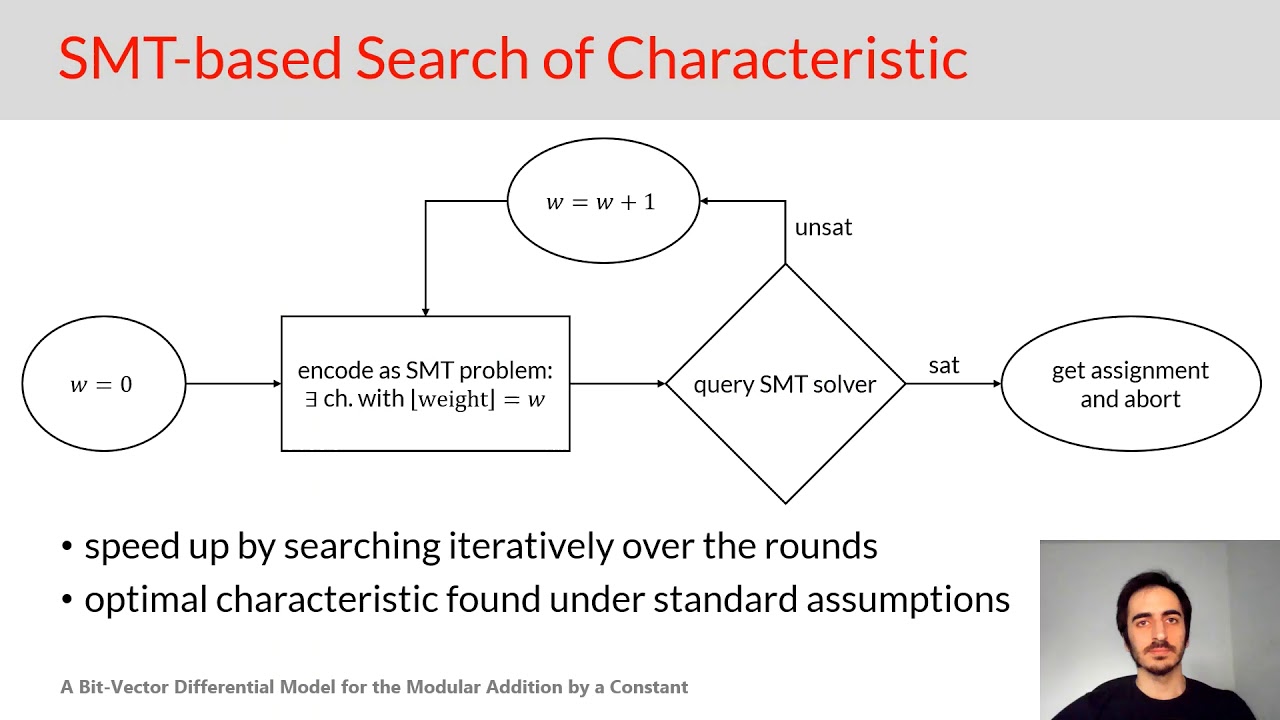
Abstract:ARX algorithms are a class of symmetric-key algorithms constructed by Addition, Rotation, and XOR, which achieve the best software performances in low-end microcontrollers. To evaluate the resistance of an ARX cipher against differential cryptanalysis and its variants, the recent automated methods employ constraint satisfaction solvers, such as SMT solvers, to search for optimal characteristics. The main difficulty to formulate this search as a constraint satisfaction problem is obtaining the differential models of the non-linear operations, that is, the constraints describing the differential probability of each non-linear operation of the cipher. While an efficient bit-vector differential model was obtained for the modular addition with two variable inputs, no differential model for the modular addition by a constant has been proposed so far, preventing ARX ciphers including this operation from being evaluated with automated methods. In this paper, we present the first bit-vector differential model for the n-bit modular addition by a constant input. Our model contains O(log_2(n)) basic bit-vector constraints and describes the binary logarithm of the differential probability. We also represent an SMT-based automated method to look for differential characteristics of ARX, including constant additions, and we provide an open-source tool ArxPy to find ARX differential characteristics in a fully automated way. To provide some examples, we have searched for related-key differential characteristics of TEA, XTEA, HIGHT, and LEA, obtaining better results than previous works. Our differential model and our automated tool allow cipher designers to select the best constant inputs for modular additions and cryptanalysts to evaluate the resistance of ARX ciphers against differential attacks.
ePrint: https://eprint.iacr.org/2020/1025
Talk: https://www.youtube.com/watch?v=fKlaDl0rxFo
Slides: https://iacr.org/submit/files/slides/2020/asiacrypt/ac2020/233/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .