Welcome to the resource topic for 2020/1022
Title:
Polynomial IOPs for Linear Algebra Relations
Authors: Alan Szepieniec, Yuncong Zhang
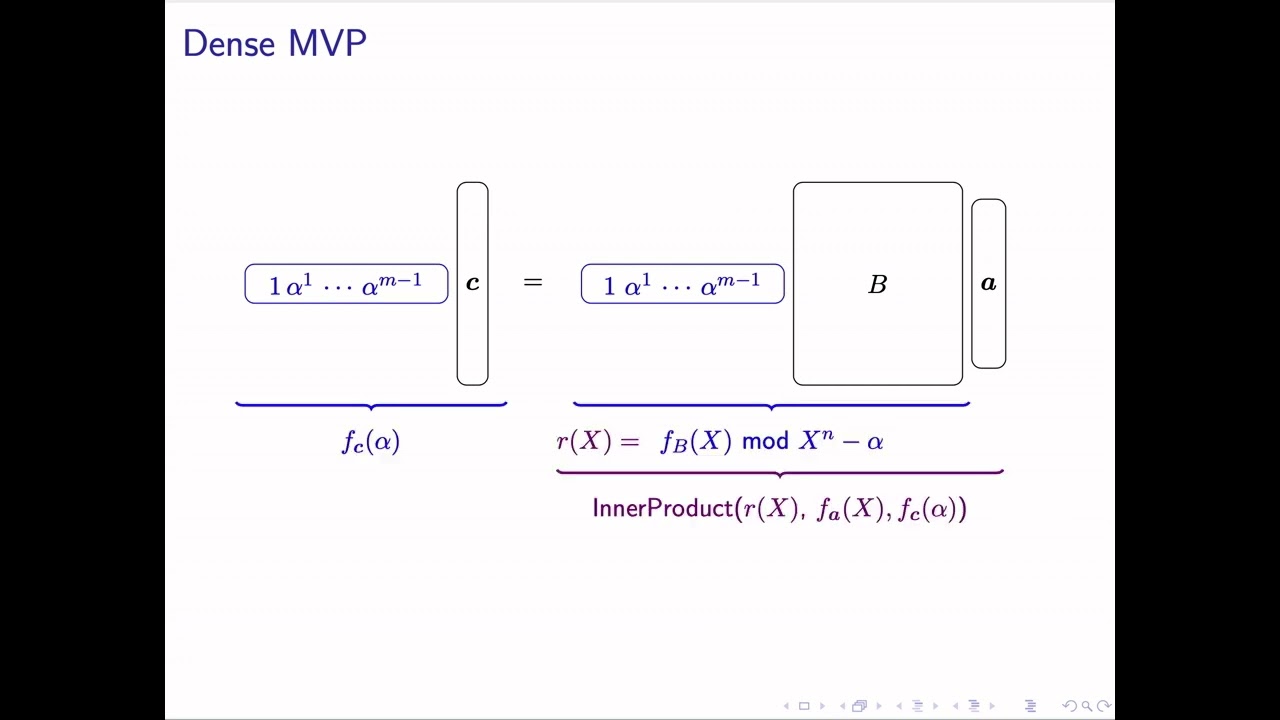
Abstract:This paper proposes new Polynomial IOPs for arithmetic circuits. They rely on the monomial coefficient basis to represent the matrices and vectors arising from the arithmetic constraint satisfaction system, and build on new protocols for establishing the correct computation of linear algebra relations such as matrix-vector products and Hadamard products. Our protocols give rise to concrete proof systems with succinct verification when compiled down with a cryptographic compiler whose role is abstracted away in this paper. Depending only on the compiler, the resulting SNARKs are either transparent or rely on a trusted setup.
ePrint: https://eprint.iacr.org/2020/1022
Talk: https://www.youtube.com/watch?v=Zt9FoDUtQUo
Slides: https://iacr.org/submit/files/slides/2022/pkc/pkc2022/15/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .