Welcome to the resource topic for 2019/1177
Title:
Proofs for Inner Pairing Products and Applications
Authors: Benedikt Bünz, Mary Maller, Pratyush Mishra, Nirvan Tyagi, Psi Vesely
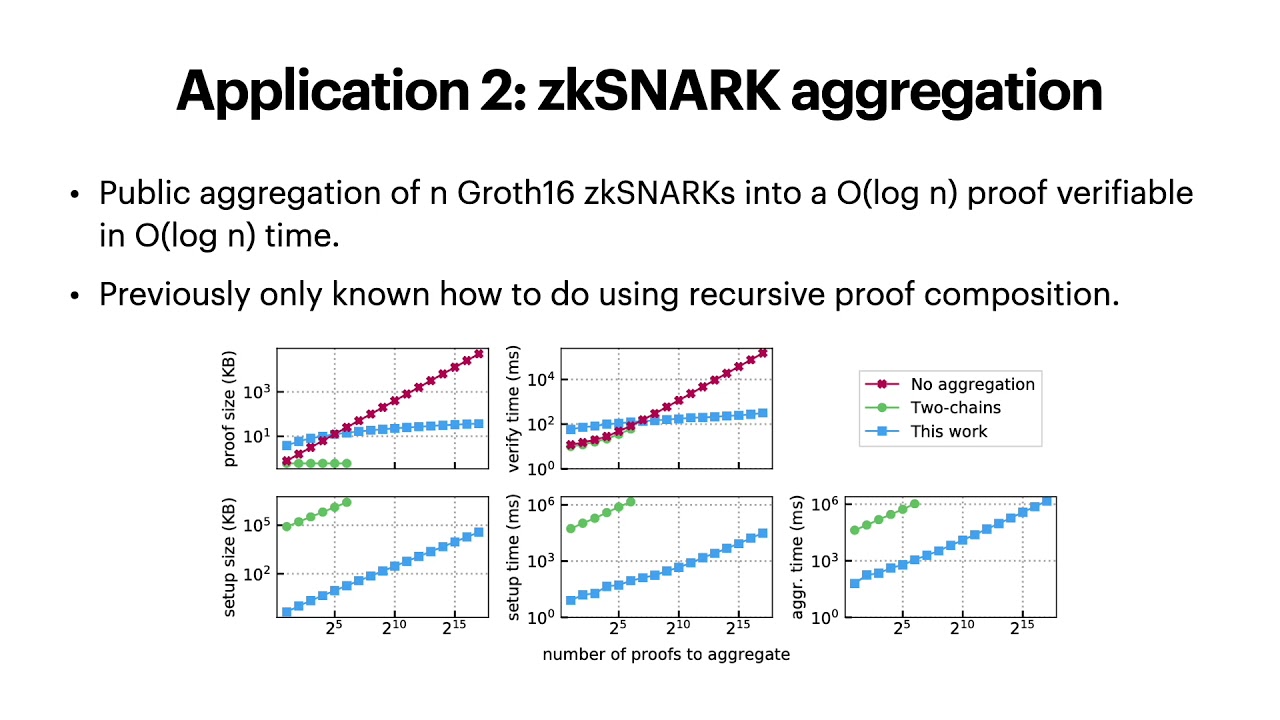
Abstract:We present a generalized inner product argument and demonstrate its applications to pairing-based languages. We apply our generalized argument to proving that an inner pairing product is correctly evaluated with respect to committed vectors of n source group elements. With a structured reference string (SRS), we achieve a logarithmic-time verifier whose work is dominated by 6 \log n target group exponentiations. Proofs are of size 6 \log n target group elements, computed using 6n pairings and 4n exponentiations in each source group. We apply our inner product arguments to build the first polynomial commitment scheme with succinct (logarithmic) verification, O(\sqrt{d}) prover complexity for degree d polynomials (not including the cost to evaluate the polynomial), and a CRS of size O(\sqrt{d}). Concretely, this means that for d=2^{28}, producing an evaluation proof in our protocol is 76\times faster than doing so in the KZG commitment scheme, and the CRS in our protocol is 1,000\times smaller: $13$MB vs $13$GB for KZG. This gap only grows as the degree increases. Our polynomial commitment scheme is applicable to both univariate and bivariate polynomials. As a second application, we introduce an argument for aggregating n \mathsf{Groth16} zkSNARKs into an O(\log n) sized proof. Our protocol is significantly more efficient than aggregating these SNARKs via recursive composition (BCGMMW20): we can aggregate about 130,000 proofs in $25$min, while in the same time recursive composition aggregates just 90 proofs. Finally, we show how to apply our aggregation protocol to construct a low-memory SNARK for machine computations. For a computation that requires time T and space S, our SNARK produces proofs in space \tilde{\mathcal{O}}(S+T), which is significantly more space efficient than a monolithic SNARK, which requires space \tilde{\mathcal{O}}(S \cdot T).
ePrint: https://eprint.iacr.org/2019/1177
Talk: https://www.youtube.com/watch?v=CxpxUlU5oEk
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .