Welcome to the resource topic for 2012/404
Title:
Secret Sharing Schemes for Very Dense Graphs
Authors: Amos Beimel, Oriol Farràs, Yuval Mintz
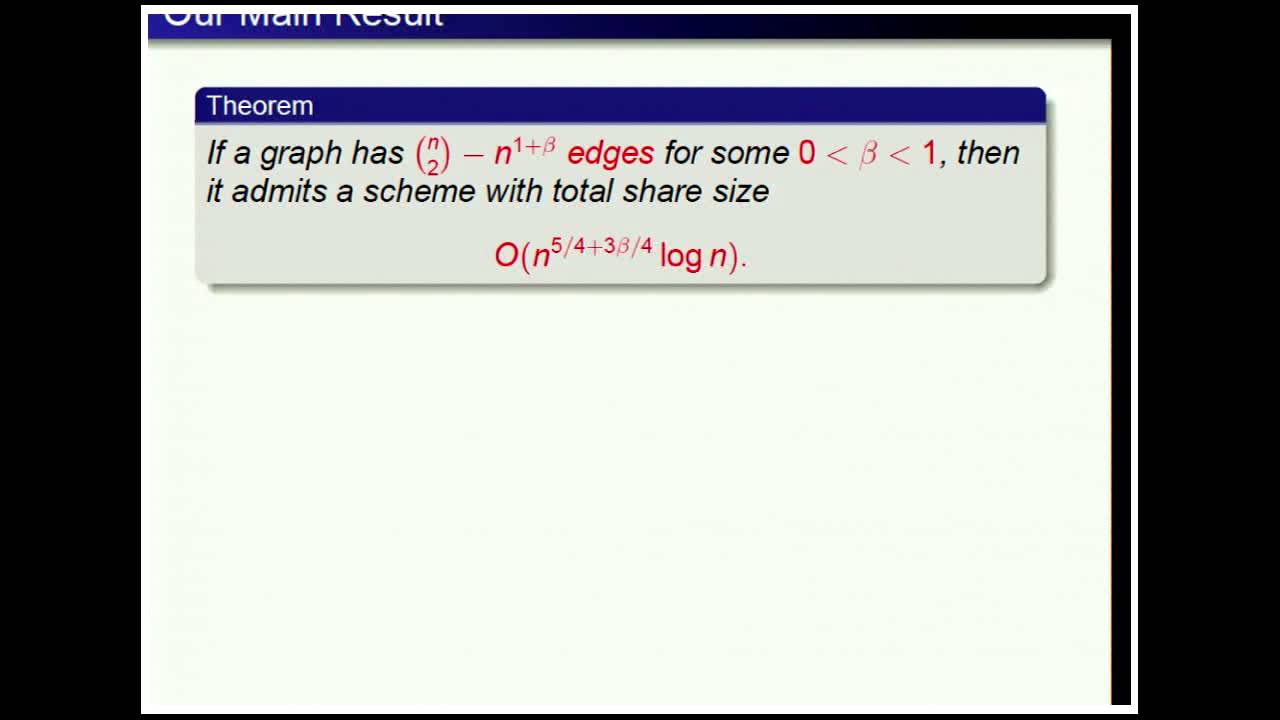
Abstract:A secret-sharing scheme realizes a graph if every two vertices connected by an edge can reconstruct the secret while every independent set in the graph does not get any information on the secret. Similar to secret-sharing schemes for general access structures, there are gaps between the known lower bounds and upper bounds on the share size for graphs. Motivated by the question of what makes a graph hard'' for secret-sharing schemes (that is, require large shares), we study very dense graphs, that is, graphs whose complement contains few edges. We show that if a graph with $n$ vertices contains $\binom{n}{2}-n^{1+\beta}$ edges for some constant $0\leq\beta <1$, then there is a scheme realizing the graph with total share size of $\tilde{O}(n^{5/4+3\beta/4})$. This should be compared to $O(n^2/\log n)$ -- the best upper bound known for the share size in general graphs. Thus, if a graph is hard’', then the graph and its complement should have many edges. We generalize these results to nearly complete k-homogeneous access structures for a constant k. To complement our results, we prove lower bounds for secret-sharing schemes realizing very dense graphs, e.g., for linear secret-sharing schemes we prove a lower bound of \Omega(n^{1+\beta/2}) for a graph with \binom{n}{2}-n^{1+\beta} edges.
ePrint: https://eprint.iacr.org/2012/404
Talk: https://www.youtube.com/watch?v=-Jic_aR0dsY
Slides: https://iacr.org/cryptodb/archive/2012/CRYPTO/presentation/2-4-Farras.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .