Welcome to the resource topic for 2020/144
Title:
Double-Base Chains for Scalar Multiplications on Elliptic Curves
Authors: Wei Yu, Saud Al Musa, Bao Li
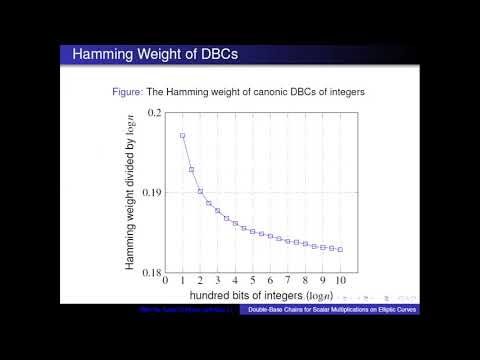
Abstract:Double-base chains (DBCs) are widely used to speed up scalar multiplications on elliptic curves. We present three results of DBCs. First, we display a structure of the set containing all DBCs and propose an iterative algorithm to compute the number of DBCs for a positive integer. This is the first polynomial time algorithm to compute the number of DBCs for positive integers. Secondly, we present an asymptotic lower bound on average Hamming weights of DBCs \frac{\log n}{8.25} for a positive integer n. This result answers an open question about the Hamming weights of DBCs. Thirdly, we propose a new algorithm to generate an optimal DBC for any positive integer. The time complexity of this algorithm is \mathcal{O}\left(\left(\log n\right)^2 \log\log n\right) bit operations and the space complexity is \mathcal{O}\left(\left(\log n\right)^{2}\right) bits of memory. This algorithm accelerates the recoding procedure by more than 6 times compared to the state-of-the-art Bernstein, Chuengsatiansup, and Lange’s work. The Hamming weights of optimal DBCs are over 60% smaller than those of NAFs. Scalar multiplication using our optimal DBC is about 13% faster than that using non-adjacent form on elliptic curves over large prime fields.
ePrint: https://eprint.iacr.org/2020/144
Talk: https://www.youtube.com/watch?v=jAlYxOQGgWg
Slides: https://iacr.org/submit/files/slides/2020/eurocrypt/ec2020/107/slides.pdf
See all topics related to this paper.
Feel free to post resources that are related to this paper below.
Example resources include: implementations, explanation materials, talks, slides, links to previous discussions on other websites.
For more information, see the rules for Resource Topics .